|
|
|
|
|
|
|
|
|
Rolle's Theorem and the Mean Value Theorem
Intermediate Value Theorem and Location Principle both apply to provide information about existence of tangent lines or, which is the same, derivatives of functions. What results is two formulations of the Mean Value Theorem of which one is more general but both are equivalent.
Theorem 1 (T1, Rolle's Theorem)
Let, for two real a and b, a < b, a function f be differentiable on a closed interval [a, b] such
that 
[a, b] such that the
line tangent to the graph of f at the point x0 is horizontal, i.e. f'(x0) = 0.
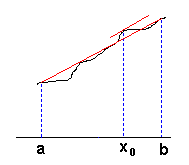
Theorem 2 (T2, Mean Value Theorem)
Let, for two real a and b, a < b, a function f be differentiable on a closed interval [a, b].
Then there exists a number x0[a, b]
such that the line tangent to the graph of f at the point x0 is parallel to the chord
connecting the two end points of the graph - (a, f(a)) and (b, f(b)).
Clearly T1 is only a special case of T2. However it's interesting that the more general T2 could be deduced from its special case, T1. Introduce a new function
| (2) |
|
Then it follows that g(a) = f(a) - (f(a) + 0) = 0 whereas
| (2) |
|
Therefore, g(a)=g(b)=0 and we can apply T1 since g is also continuously
differentiable on [a, b]. Therefore, there exists x0[a, b] such that
Q.E.D.
(There is a second, more extended, attempt, on this topic that is accompanied by an interactive Java illustration.)
Copyright © 1996-2008 Alexander Bogomolny
| 28676920 |  |
|