Expressions Invariant under Projective Mappings
Three concurrent cevians in a triangle remain concurrent if the whole plane undergoes a perspective transformation. This tells us that, if such a transformation maps a generic point $X$ to $X'$ and, for $\Delta ABC$ and points $D$, $E,$ $F$ on $BC,$ $AC,$ and $AB,$ respectively, $\displaystyle\frac{AF}{FB}\cdot\frac{BD}{DC}\cdot\frac{CE}{EA}=1$ then also $\displaystyle\frac{A'F'}{F'B'}\cdot\frac{B'D'}{D'C'}\cdot\frac{C'E'}{E'A'}=1,$ implying that Ceva's theorem remains valid under perspective transformations.
Similar claims hold for Menelaus' theorem, and the cross-ratio, harmonic ratio, in particular.
I am going to prove a general statement [Howard Eves, 247-249] concerning expressions that appear in the just mentioned theorems:
Assume we have an expression (as above) that includes products and ratios of signed segments and that this expression has the two following properties:
If we replace a generic segment $XY$ with $X\times Y,$ for all segments involved, and regard the resulting expression as an algebraic one, all the individual letters will cancel out.
If we replace a generic segment $XY$ by a single symbol, say $x,$ representing the line on which the segment is found, apply this procedure to all the segments involved, and then regard the resulting expression as an algebraic one, all letters will cancel out.
Then the value of such an expression is invariant under any perspective mapping.
If the theorem holds, the value of the expression will remain invariant under a sequence of perspective mappings, which are known as projectivities.
Proof
Let $V$ be the center of perspectivity and $XY$ one of the segments in the expression at hand that is mapped onto segment $X'Y'.$ Let $p$ denote the distance from $V$ to $XY$ and $p'$ the distance from $V$ to $X'Y'.$ (We also assume $p\ne 0.)$ Then
$p\cdot XY=VX\cdot VY\cdot\mbox{sin}(\angle XVY),$
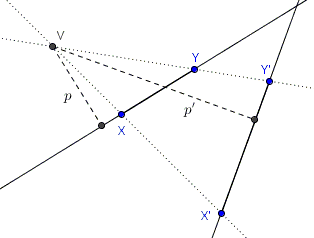
since each side is twice the area of $\Delta XVY.$ Therefore, $XY=VX\cdot VY\cdot\mbox{sin}(\angle XVY)/p.$ Now, apply this result to all the segments in the given expression. Due to the first stipulated property, all the segments $VX, $ etc., will cancel out; due to the second property, all $p'\mbox{s}$ will cancel out, leaving only the $\mbox{sin's}$ of the angles involved. But $\angle XVY=\angle X'VY'$ for all such angles. So working backwards, and putting in $p'$ and $X'Y'\mbox{s}$ in the former locations of the corresponding $p$ and $XY\mbox{s}$ would not change the value of the expression because these would cancel exactly as the non-primed segments.
This proves the statement.
Examples
Ceva's theorem. A triangle and a point can be projectively mapped onto a triangle and its centroid. For the latter Ceva's theorem trivially holds. Hence it holds for any triangles.
Menelaus' theorem. Project line $DEF$ to infinity, causing
$\displaystyle\frac{B'D'}{D'C'}=\frac{C'E'}{E'A'}=\frac{A'F'}{F'B'}=-1,$
and, implying,
$\displaystyle\frac{B'D'}{D'C'}\cdot \frac{C'E'}{E'A'}\cdot \frac{A'F'}{F'B'}=-1.$
Which shows that Menelaus' theorem is valid in this case and, therefore, for any other triangle and transversal.
Cross-ratio. The cross ratio $(ABCD)$ of four collinear points is defined as $(ABCD)=\displaystyle\frac{CA}{CB}:\frac{DA}{DB}$ which clearly satisfies the first condition of the above theorem. The second condition need not be satisfied for collinear points (which makes all $p$ equal so that - in the proof - they cancel out automatically), implying that the cross-ratio remains invariant under projective mappings.
Harmonic ratio. Four points are in harmonic ratio if their cross ratio equals $-1.$ The theorem says that points remain in harmonic ratio under projective transformations.
Pascal's Hexagon. Pascal's Hexagon appears to have an extra, previously undocumented, property.
Pappus' and Desargues' theorems can also be established on the basis of the above statement.
References
- H. Eves, A Survey of Geometry, Allyn and Bacon, Inc. 1972
Related material
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
![]()
|Contact| |Front page| |Contents| |Generalizations| |Arithmetic|
Copyright © 1996-2018 Alexander Bogomolny
73580302
