A Property of Pascal's Hexagon Pascal May Have Overlooked
On January 3, 2014, Dao Thanh Oai posted the following theorem at CutTheKnot facebook page. He dubbed it Viet Nam Theorem as well he might; for, I believe the theorem that deals with Pascal's hexagon has been likely overlooked by Pascal himself and the generations of geometers ever since.
Theorem
Given hexagon $ABCDEF,$ let $AB$ meet $DE$ at $G,$ $BC$ meet $EF$ at $H,$ $AF$ meets $CD$ at $I:$
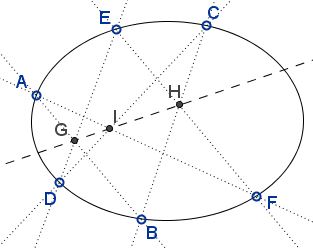
Then, as well known, the six vertices of the hexagon lie on a conic iff the points $G,$ $H,$ $I$ are collinear. In addition, the two conditions imply
(*)
$\displaystyle\frac{AG}{GB}\cdot\frac{BH}{HC}\cdot\frac{CI}{ID}\cdot\frac{DG}{GE}\cdot\frac{EH}{HF}\cdot\frac{FI}{IA}=1.$
Proof
The assertion of the theorem has been discovered experimentally with the GeoGebra. As shown by Hubert Shutrick its veracity is implied by the general property of what Howard Eves termed h-expressions [Survey, p. 247]. The details can be found on an earlier page at this site.
References
- H. Eves, A Survey of Geometry, Allyn and Bacon, Inc. 1972
Related material
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
![]()
|Contact| |Front page| |Contents| |Generalizations| |Arithmetic|
Copyright © 1996-2018 Alexander Bogomolny
73580583
