Dissection of Triangle into Rhombus
The applet below illustrates Problem 8 from the 2010 All-Russian Olympiad:
The problem has been brought to my attention by Vo Duc Dien who also supplied a lovely solution:

Dien's solution (see also his post elsewhere) assumes that the three parts mentioned in the problem have been obtained by straight line cuts. I believe this is a very natural interpretation with which I am in complete agreement. The applet implements Dien's construction. To lead to a rhombus, the cuts from points E and F to BC need to be EF/2 in length; otherwise, the resulting shape is a mere parallelogram, not a rhombus.
| What if applet does not run? |
At the bottom of the applet there are two scrollbars. The first rotates two triangular pieces around two vertices. The second scrollbar controls the slant of the two cuts. The cuts originate at the midpoints of two sides adjacent to a selected vertex. Pressing the "Rotate vertices" button will cycle through three vertices of the triangle changing the selection.
With the box "info" checked the applet will display the approximate measures of the angles in degrees and state whether the condition of having a median longer than a side holds at any of the vertices. Finally, it also displays the length (h) of the A-altitude and a/2. For the construction to work one needs
When the "hint" box is checked the applet displays two circles centered at E and F with the radius EF/2. The points of intersection of the circles with BC are the points to which the cuts should be made from R and F. Sometimes there are two pairs of solutions, sometimes there is just one. On occasion, the circles do not cross BC at all. In the latter cases, the construction fails to produce a rhombus.
With the help of the applet I found that the construction does not work for the triangle with angles 81.5°, 64.5°, and 34°:
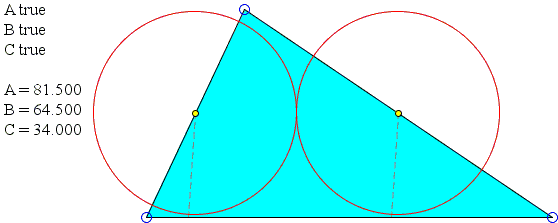
The construction fails regardless of the selected vertex, although the premises hold at any of them.
Hubert Shutrick came up with a general condition for h < a/2 to hold for all three vertices of a triangle. This follows from the Law of Sines:
In aprticular, a = 2R·sinα. For the altitude h to the side a, h = b·sinγ and using the Law of Sines:
Therefore, the condition h < a/2 is equivalent to
which needs to be considered cyclicly. However, one must not forget the basic requirement, viz.,
(There is another attempt at solving the problem.)
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73581003
