A Three Pegs Question

Three pegs on a plane form an isosceles right triangle with a leg of length 3. The pegs may move to an arbitrary distance but on a line parallel to the line formed by the other two. Is it possible to eventually get the three pegs at the vertices of a right triangle with legs 2 and 4?

---

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at http://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

---

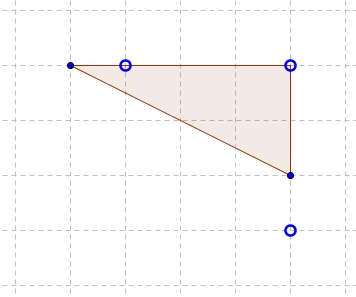
Buy this applet What if applet does not run?

Solution

No, this is not possible.

To see why, consider the triangle formed by the three pegs. The displacement of a vertex along the line parallel to the opposite side does not change the area of the triangle. In other words, the area of the triangle formed by the three pegs is invariant under any possible puzzle move. Initially, the area was 3×3/2 = 4.5. This is different from 2×4/2 = 4. Therefore, the pegs can never settle at the vertices of the other triangle.

References