5-Star and A Circle: What Is It About?
|
| Buy this applet What if applet does not run? |
|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2012 Alexander Bogomolny
A "common" 5-star defines five triangles and a pentagon. (It could be built starting with a pentagon whose sides are the extended to intersect at the vertices of a star.) Each of the five triangles is inscribed in a circle. The neighboring circles intersect at two points: a vertex of the pentagon and one other point. It's remarkable that those "other" points lie on a circle.
| Buy this applet What if applet does not run? |
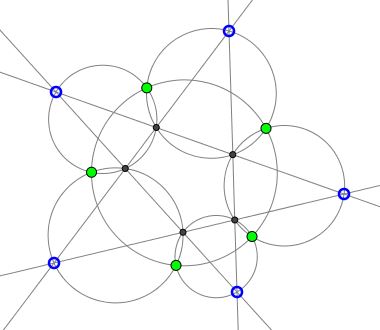
The above statement falls into a very general framework of center circle chains. Four lines define four triangles whose circumcircles meet at a point, known as Miquel's point of the 4-line. Five lines define five Miquel's points that are known to lie on a circle, Clifford's Circle of the 5-line.
The 5-star is defined by 5 lines. When one line is disregarded, the remaining four cross in such a manner as to form (among other polygons) two adjacent triangle legs of the star. Obviously, the circumcirlces of the latter intersect at Miquel's point of the 4-line. This proves the statement.
However, there are also simple direct proofs. To be continued ...
References
|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2012 Alexander Bogomolny
| 41143785 |
