Morley Constellation
Frank Morley discovered a magnificent construction of 27 equilateral triangles related to an arbitrary triangle ABC. The vertices of the triangles are formed by intersections of certain straight lines - axes associated with ΔABC. It therefore follows that the vertices of Morley's triangles serve as the points of concurrence of several straight lines. It was observed much later [Sastry] that Morley's configuration is a rich source of numerous additional concurrences.
In fact, the number of possible concurrences in the diagram is quite overwhelming. To keep the total to a manageable size, the applet below only incorporates two of Morley's triangles. One is formed at the intersections of adjacent internal trisectors (PQR in the diagram below), the other by their external counterparts (not shown, P'Q'R' in what follows)
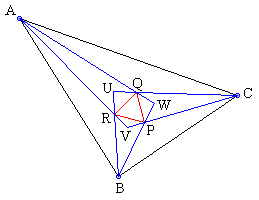
The lines PP', QQ', RR' are concurrent. Put differently, triangles PQR and P'Q'R' are perspective. Following is a complete list of triangles available in the applet below that may be (occasionally) mated into perspective pairs.
| ABC | | is the basic triangle whose vertices are draggable |
|---|
| PQR | | Morley's first triangle |
|---|
| P'Q'R' | | Morley's second triangle |
|---|
| UVW | | triangle obtained at the intersection of not adjacent trisectors |
|---|
| U'V'W' | | similar to UVW, but formed by the external trisectors |
|---|
| LLL (ABC-PQR) | | Formed by points of intersection of angle bisectors of ΔABC with the corresponding sides of ΔPQR |
|---|
| LLL (PQR-ABC) | | Formed by points of intersection of angle bisectors of ΔPQR with the corresponding sides of ΔABC |
|---|
| LLL (AQC-AC) | | Formed by points of intersection of the bisectors of angles AQC, CPB, and BRA with sides AC, CB, and BA of ΔABC |
|---|
| AAA (ABC-PQR) | | Formed by points of intersection of perpendiculars from vertices ABC to the corresponding sides of ΔPQR |
|---|
| AAA (PQR-ABC) | | Formed by points of intersection of perpendiculars from vertices PQR to the corresponding sides of ΔABC |
|---|
| LLL (ABC-P'Q'R') | | Formed by points of intersection of angle bisectors of ΔABC with the corresponding sides of ΔP'Q'R' |
|---|
| LLL (P'Q'R'-ABC) | | Formed by points of intersection of angle bisectors of ΔP'Q'R' with the corresponding sides of ΔABC |
|---|
| LLL (AQ'C-AC) | | Formed by points of intersection of the bisectors of angles AQ'C, CP'B, and BR'A with sides AC, CB, and BA of ΔABC |
|---|
| AAA (ABC-P'Q'R') | | Formed by points of intersection of perpendiculars from vertices ABC to the corresponding sides of ΔP'Q'R' |
|---|
| AAA (P'Q'R'-ABC) | | Formed by points of intersection of perpendiculars from vertices P'Q'R' to the corresponding sides of ΔABC |
|---|
| III (QAR) | | Formed by the incenters of triangles QAR, RBP, PCQ |
|---|
| III (ABR) | | Formed by the incenters of triangles ABR, BCP, CAQ |
|---|
| OOO (QAR) | | Formed by the circumcenters of triangles QAR, RBP, PCQ |
|---|
| OOO (ABR) | | Formed by the circumcenters of triangles ABR, BCP, CAQ |
|---|
| III (Q'AR') | | Formed by the incenters of triangles Q'AR', R'BP', P'CQ' |
|---|
| III (ABR') | | Formed by the incenters of triangles ABR', BCP', CAQ' |
|---|
| OOO (Q'AR') | | Formed by the circumcenters of triangles Q'AR', R'BP', P'CQ' |
|---|
| OOO (ABR') | | Formed by the circumcenters of triangles ABR', BCP', CAQ' |
|---|
| HHH (QAR) | | Formed by the orthocenters of triangles QAR, RBP, PCQ |
|---|
| HHH (ABR) | | Formed by the orthocenters of triangles ABR, BCP, CAQ |
|---|
| HHH (Q'AR') | | Formed by the orthocenters of triangles Q'AR', R'BP', P'CQ' |
|---|
| HHH (ABR') | | Formed by the orthocenters of triangles ABR', BCP', CAQ' |
|---|
In addition, the applet allows one to consider pairs of isogonal lines instead of two angle trisectors. This is achieved by clicking on the numerator and the denominator of the fraction at the bottom of the applet. Numbers increase/decrease if clicked on to the left/right of their central vertical lines. The number that may be displayed in the upper left corner of the applet is the area of the triangle formed by three straight lines whose concurrence is being investigated. The number, of course, is only approximate.
(Some of the triangles have already been considered elsewhere.
For some proofs, see the page Of Looking and Seeing.
References
- K. R. S. Sastry, Constellation Morley, Math Mag 47 (1974) 15-22
|Activities|
|Contact|
|Front page|
|Contents|
|Geometry|
Copyright © 1996-2018 Alexander Bogomolny

