Two Common Chords in Three Concurrent Circles

Points \(N, P, Q\) are collinear. For a fourth point \(M,\) consider circumcircles, \((A)\) of \(\Delta MNP\), \((B)\) of \(\Delta MPQ\), \((C)\) of \(\Delta NPQ.\) \(D\) a point on \((B)\), \(F=DM\cap (A),\) \(G=FN\cap (C).\)

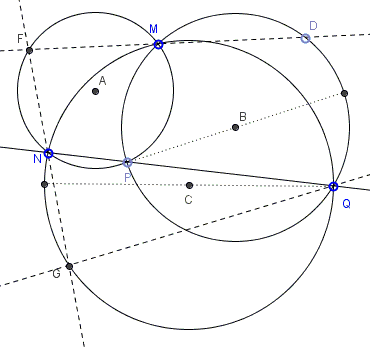
In three concurrent circles Two Common chords join end-to-end. Their configuration is closely related to the corresponding diameters - problem

Prove that, if one of the segments \(DP\), \(FP\), \(GQ\) is a diameter in the respective circle, so are the other two.

(The applet below illustrates the problem.)

Created with GeoGebra

Solution

Solution

Prove that, if one of the segments \(DP\), \(FP\), \(GQ\) is a diameter in the respective circle, so are the other two.

If \(DP\) is a diameter of \((B)\) then, as we know, \(FP\) is a diameter of \((A),\) and vice versa.

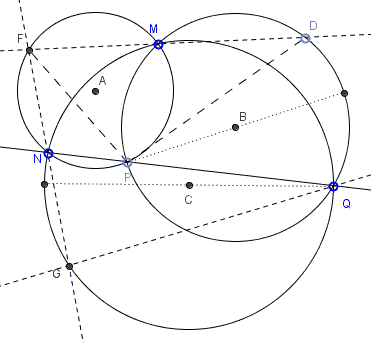
In three concurrent circles Two Common chords join end-to-end. Their configuration is closely related to the corresponding diameters - solution

If \(FP\) is a diameter of \((A)\) then angle \(FNP\) is right. \(FN\perp NP\), which is the same as \(GN\perp NQ\) so that \(GQ\) is a diameter of \((C),\) and vice versa.

72187094