Exeter Point
Sohail Farhangi
17 February, 2013
The Exeter point - being found in 1986 - is a relatively recent discovery in triangle geometry. Elsewhere we established the following theorem:
Let the incircle \(T\), of \(\Delta ABC\) be tangent to the sides at \(A'\), \(B'\), and \(C'\) as shown below. For a point \(P\) in the plane, let \(AP\), \(BP\), and \(CP\) intersect \(T\) at \(A_1\), \(B_1\), and \(C_1\) respectively. Then \(AA_1\), \(BB_1\), and \(CC_1\) concur at a point \(P'\).
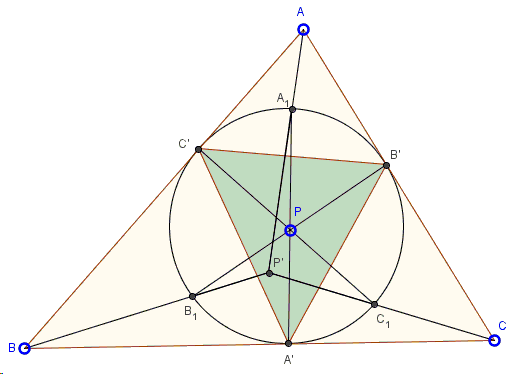
The Exeter point \(E=P'\) for \(P\) being the center \(G\) of a triangle. Below we prove an important property of Exeter point, to boot:
The Exeter point \(E\) lies on the Euler line \(L\) of \(\Delta A'B'C'\).
The applet below serves a dynamic illustration:
Proof
Let \(M_A\), \(M_B\), \(M_C\) be the midpoints of sides \(BC\), \(CA\), \(AB\), respectively. We begin by inverting lines \(AA_1\), \(BB_1\), and \(CC_1\) with respect to \(T\). Noting that \(AB'\) and \(AC'\) are tangent to \(T\), we can see that \(A\) maps to \(M_A\) under our inversion, and the same can be seen for vertices \(B\) and \(C\). Points \(A_1\), \(B_1\), and \(C_1\) are invariant under the inversion as they lie on \(T\). We may also note that the point at infinity on lines \(AA_1\), \(BB_1\), \(CC_1\) map to the incenter \(I\) under our inversion. We can now see that lines \(AA_1\), \(BB_1\), \(CC_1\) map to circles \(A_{1}M_{A}I\), \(B_{1}M_{B}I\), and \(C_{1}M_{C}I\) under our inversion, which will be referred to as \(O_A\), \(O_B\) and \(O_C\), respectively.
Noting that the center of \(T\) is the circumcenter of \(\Delta A'B'C'\), which is on \(L\), we know that \(E\) lies on \(L\) if and only if \(E'\), the image of \(E\) under our inversion also lies on \(L\). From the definition, \(O_A\), \(O_B\), \(O_C\) concur at \(E'\). Therefore, we only need to show that \(G\) is on the radical axis of \(O_A\), \(O_B\), \(O_C\), which can be done by showing that it has the same power with respect to any \(2\) of these \(3\) coaxial circles.
For the next step we prove the following
Lemma
\(M_{B}M_{C}C_{1}B_{1}\) is a cyclic quadrilateral.
Proof
\(C'B'C_{1}B_{1}\) is a cyclic quadrilateral, so \(C'B'\) and \(B_{1}C_{1}\) are antiparallel lines. Let the circumcircle of \(\Delta B_{1}M_{B}C_{1}\) intersect \(\Delta A'B'C'\) at \(M'_C\). \(M_{B}M'_C\) and \(B_{1}C_{1}\) are also antiparallel lines, which implies that \(M_{B}M'_{C}\) and \(B'C'\) are parallel lines, so \(M'_{C} = M_C\) as desired.
Returning to the main proposition, we can see that \(B_{1}M_{B}\) and \(C_{1}M_{B}C\) intersect at \(G\) by definition. Applying Lemma tells us that \(GM_{B} \times GB_{1} = GM_{C} \times GC_{1}\) as desired.
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73573713
