François Viète's Reduction of CCC to PCC

The original treatment of what is now known as the Problem of Apollonius was the subject of two lost books The Tangencies by Apollonius of Perga (c. 262-190 BC). In the sixteens century a French mathematician François Viète (1540-1603) made an attempt to reconsruct Apollonius' proofs. One of the devices he came up with was reducing the problem in one configuration to another. The reduction of LCC to PLC serves one example. Below I present Viète's similar reduction of the CCC problem to the PCC variant.

Find a circle tangent to three given circles \((A)\), \((E)\) and \((C):\)

Construct a circle tangent to three given circles

(The applet below illustrates the construction for the case where Apollonius' circle have the same kind of tangency with the given three circles - either all internal or all external.)

Solution

Construction

Find a circle tangent to three given circles \((A)\), \((E)\) and \((C):\)

Construct a circle tangent to three given circles

Assume that radii of circles \((A)\), \((C)\) and \((E)\) are \(a,\) \(c,\) and \(e,\) respectively, and that \(a\) is the least of the three (or, more accurately, not the largest.) Then, as shown in the diagram, the original three-circle (CCC) problem may be reduced to finding a circle tangent to two given circles and passing through a given point - the PCC problem.

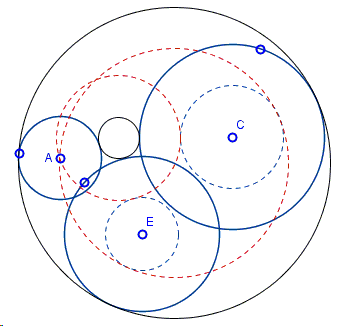
Construct a circle tangent to three given circles - solution

The diagram (as the applet above) illustrates the case where Apollonius' circle have the same kind of tangency with the given three circles - either all internal or all external. Adjustments are required for the other six cases, but the general idea remains the same.

Thus assuming \(a\lt e, c\), form circles \((C,c-a)\) with center \(C\) and radius \(c-a\) and circle \((E,e-a)\) with center \(E\) and radius \(e-a\) We may now may solve the PCC problem with point \(A\) and circles \((C,c-a)\) and \((E,e-a)\). If that problem has a solution \((X,r)\), then either \((X, r-a)\) or \((X, r+a)\) solves the original problem.

Since the PCC problem may have four solution and each of these may lead to two CCC solution, the latter problem may have up to eight solutions.

References

N. Altshiller-Court, College Geometry, Dover, 1980, #516
J. Hadamard, Lessons in Geometry, AMS, 2008, Complements to Book III, Ch. VI
R. A. Johnson, Advanced Euclidean Geometry (Modern Geometry), Dover, 1960, #167

71543065