PCC: Apollonius' Problem with Two Circles and a Point

Each of the cases of the Problem of Apollonius has several known solutions. The problem with three circles (CCC) may be reduced to the problem with two circles and a point (PCC). As I shall show below, the latter reduces to an even more special case, that of two points and a circle (PPC).

Find a circle tangent to two given circles and passing through a given point:

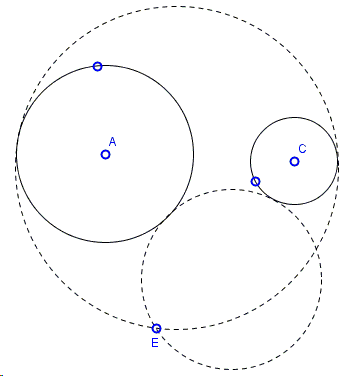
Find a circle tangent to two given circles and passing through a given point - problem

The applet below illustrates the construction. The given circles are \((A)\) and \((C)\) and \(E\) is the given point. Both circles have a nameless point on the boundary that can be dragged to modify the circle.

Solution

Construction

Find a circle tangent to two given circles and passing through a given point:

Find a circle tangent to two given circles and passing through a given point - problem

A simple remark shows that the problem can be reduced to the PPC case. Indeed, a circle tangent to two given circles and passing through a given point, passes necessarily through another point that can be easily found:

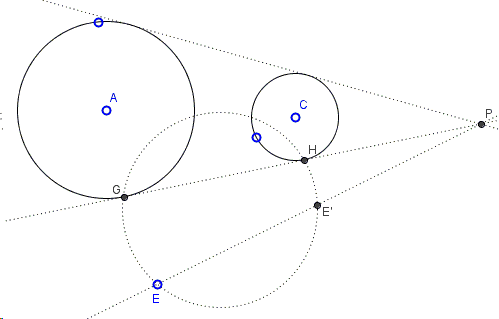
Find a circle tangent to two given circles and passing through a given point - problem

Let \(P\) be (in our case) external center of similitude of the given circles \((A)\) and \((C)\), with the common tangent through \(P\) touching \((A)\) at \(G\) and \((C)\) at \(H\). Form the circumcircle \(EGH.\) Let \(E'\) be a second intersection of \(EP\) with \(EGH.\) Then

\( EP\cdot E'P = GP\cdot HP \)

which is in fact a given. Thus point \(E'\) can be easily determined; the task now becomes finding a circle through points \(E\) and \(E'\) tangent to any of the given two circles. The diagram below combines all the steps of the construction:

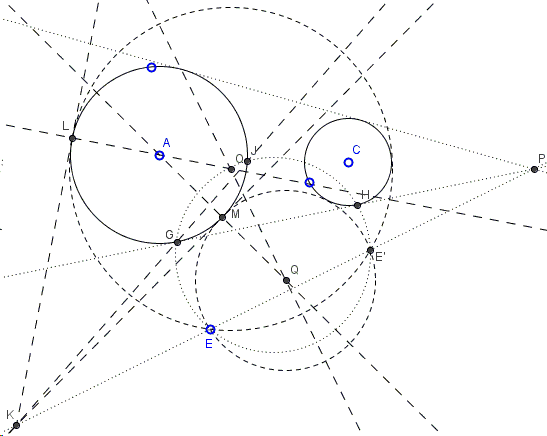
Find a circle tangent to two given circles and passing through a given point - solution

Note that above we have looked into the case where the sought circles touch the given ones in the same sense - either both internally or both externally. There may be two other possibilities, increasing the total number of solutions from 2 to 4:

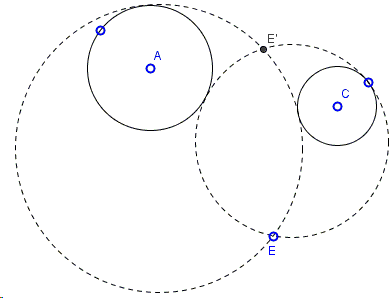
Find a circle tangent to two given circles and passing through a given point - internal tangents

To obtain these solution one has to start with the internal center of similitude of the two given circles. I have also overlooked the case where one of the circles lies entirely within the other, in which case finding the common tangents is of no help. This case will be illustrated separately.

References

N. Altshiller-Court, College Geometry, Dover, 1980, #513
J. Casey, A Sequel to the First Six Books of the Elements of Euclid, University of Michigan, 2005 (reprint of 1888 edition), Book VI, Section V, Proposition 10, Corollary 2
J. L. Coolidge, A Treatise On the Circle and the Sphere, AMS - Chelsea Publishing, 1971, p. 169
J. Hadamard, Lessons in Geometry, AMS, 2008, Complements to Book III, Ch. VI
R. A. Johnson, Advanced Euclidean Geometry (Modern Geometry), Dover, 1960, #168

70767601