LCC: Apollonius' Problem with Two Circles and a Line

Below I give an elementary Euclidean construction to a variant of the Problem of Apollonius:

Find a circle tangent to two given circles \((A)\) and \((B)\) and a given line \(m\):

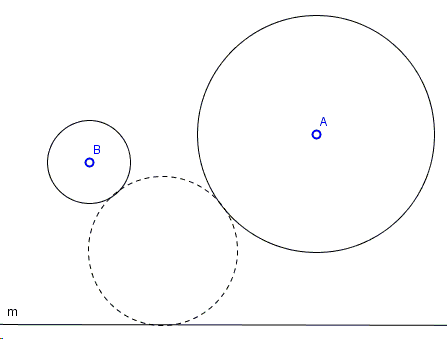
Construct a circle tangent to two given circles and a given line

(The applet below illustrates the construction.)

Solution

Construction

Find a circle tangent to two given circles \((A)\) and \((B)\) and a given line \(m\):

Construct a circle tangent to two given circles and a given line

Assume that radii of circles \((A)\) and \((B)\) are \(a\) and \(b\), respectively, and that \(b\lt a.\)

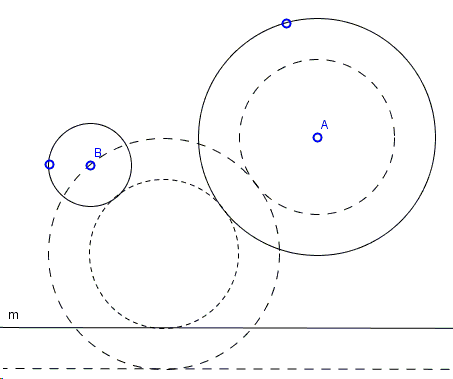
Construct a circle tangent to two given circles and a given line - solution

Form circle \((A,a-b)\) with center \(A\) and radius \(a-b.\) Also, shift line \(m\) away from the two circles to position \(m_b\), at distance \(b\) from \(m.\) We may now may solve the PLC problem with point \(B\), line \(m_b\), and circle \((A,a-b)\). If that problem has a solution \((X,r)\), then \((X, r-b)\) solves the original problem.

Since the PLC problem has four solution and line \(m\) can be moved in either of the two directions, the problem may have up to 8 solutions.

References

N. Altshiller-Court, College Geometry, Dover, 1980, #515

72106360