CCC: Apollonius' Problem with Three Intersecting Circles
Hubert Shutrick came up with a solution of the Problem of Apollonius in the case two of the three circles intersect:
Find a circle tangent to three given circles
Elsewhere it is pointed out that the general case can be reduced to the special case LLC by inverting with respect to a circle centered at one of the intersection points, constructing the circle in the special case and then inverting back. It is less complicated to imitate the special construction without transforming. Here is the LLC construction:
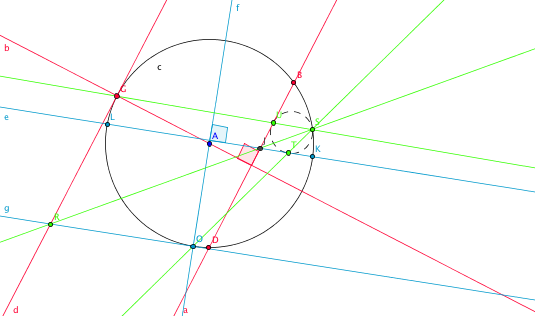
Imagine now that a sphere has been placed on the plane and the three circles are projected onto it by stereographic projection, after which the sphere is rolled so that the image of one of the intersection points of the two circles is the top point and then projected down again. It should then resemble the diagram above. We now imitate the construction above for the three circles remembering that lines above correspond to circles. The circle corresponding to the line \(AG\) above is determined as being orthogonal to the two circles involved since the center \(A\) is not preserved.
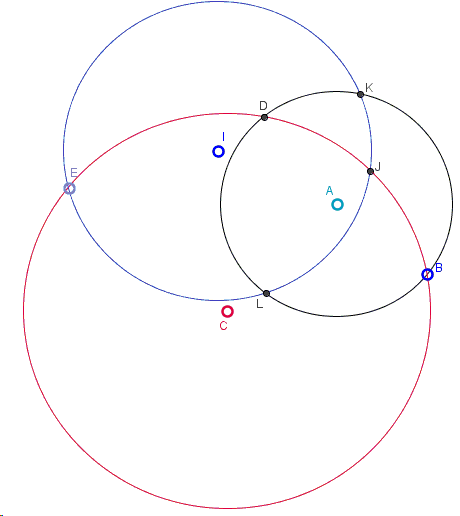
In the diagram, the given circles are \(c(BDLK)\) centered \(A,\) \(d(JBDE)\) centered \(C\) and \(k(ELKJ)\) centered \(I.\) We construct the Apollonian circle in the arc triangle \(JBK\) so \(E\) corresponds to the point at infinity.
(The applet below illustrate the construction. Points \(A, B, C, E, I\) are draggable such that the configuration may be changed. But it should be changed only slightly as the configuration is rather sensitive.)
The construction proceeds in several steps:
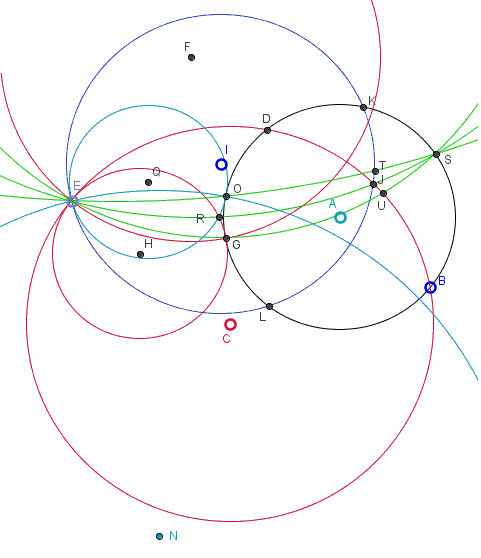
Step 1: Construct the circle \(f(EG)\) whose centered \(F\) is the intersection of the perpendicular to \(CE\) at \(E\) and \(BD,\) because it is orthogonal to \(c\) and \(d\) and because \(G\) on the circle \(c\) will be the point where a circle \(h(EGR)\) is tangent to \(c\) and will correspond to the tangent line in the special case. The centered of \(h\) is \(H\) the intersection of \(CE\) and \(AG.\)
Step 2: In the same way, the circle \(p(EO)\) centered \(N\) leads to circle \(r(EOR)\) centered \(Q\) corresponding to the other tangent. The two circles \(h\) and \(r\) have the common point \(R.\)
Step 3: The circle \(s(ERJ)\) meets the arc \(KB\) of \(c\) at the tangency point \(S\) for the required circle.
Step 4: The circles \(t(EGS)\) and \(u(EOS)\) give the other two tangency points \(U\) and \(T.\)
The circle through points \(S\), \(T\), \(U\) is inscribed into the curvilinear triangle \(JBK\).

|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73608597
