Apollonian Circle for Two Lines and a Circle
Hubert Shutrick suggested and solved a construction problem and instigated a research whether the problem has been solved elsewhere. The expectation was that due to the simplicity and elegance of the solution, there was a good chance that both the problem and the solution have already been known. A short verification proved that to be the case. This happened to be problem 13c form I. M. Yaglom's classic Geometric Transformations II.
Find a circle tangent to two given lines and a given circle:
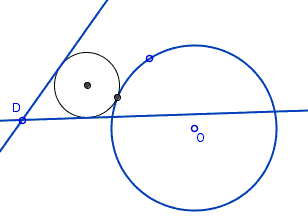
The problem is, on one hand, a specific case of the problem of Apollonius (to construct a circle tangent to three given circles) when two of the given circles have infinite radius, i.e., degenerate into straight lines. On the other hand, if two of the circles intersect, an inversion with center at their common point, reduces the problem to the one with two straight lines. Two touching circles invert into parallel lines, and this is an easy case because then the radius of the sought circle is immediately obvious. (Hubert found a way to extend the construction below to the case of three circles with no recourse to inversion.) Thus the diagram above, the applet and the proof below relate to the case where the two lines intersect.
(The applet below illustrates the proof. Points \(B,C,D,O\) and a hole unnamed point on the circle are draggable. This permits changing the configuration, but within certain limitations. While the problem may have up to eight solutions, the applet at best picks up only two.)
References
- I. M. Yaglom, Geometric Transformations II, MAA, 1968
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
Construction
Find a circle tangent to two given lines and a given circle:

Assuming that one solution has been found, what can be said about it? Two touching circles are images of each other under a homothety with center at their common point. That homothety transforms two lines tangent to the sought circle into two lines tangent to the given circle, the point of their intersection being the image of the common point of the given lines. This suggests the following construction:
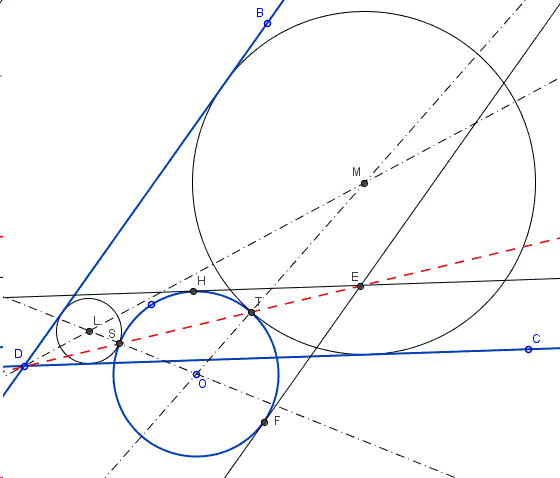
First draw tangents to the given circle parallel to the two given lines. There are choices to be made. From the two lines parallel to a given one choose that which could be its homothetic image with the center at the expected pont of tangency of two circles.
Assume the given lines intersect at \(D\) and the constructed lines in \(E\). Line \(ED\) intersect the given circle in points \(S\) and \(T\). These are going to be the centers of homothety and points of tangency of pairs of circles.
Finally, observe that the center of a sought circle is homothetic to the center of the given one, and is therefore collinear with the latter and the center of homothety. Thus we draw the line through the center of the given circle and either \(S\) or \(T\) (or both) till it intersects the bisector of the angles formed by the two given lines. In the diagram these are the points \(L\) and \(M\). One of the solutions to our problem is circle \(L(S)\) through \(S\) with center \(L\); the other \(M(T)\).
Why is it so? Consider, say, \(L(S)\). By the construction, this is a homothetic image in \(S\) of the given circle. The two circles share point \(S\) and no other. If they did, there would be a third point on a line through \(S\) the homothetic image of that one. But two circles may at most have two points in common. This validates the construction.
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73581015
