Concyclic Points in a Triangle
| What if applet does not run? |
Let AHa be the A-altitude of ΔABC, ALa the angle bisector of the angle at A, A' the midpoint of BC, P and Q the feet of perpendiculars from B and C on ALa. Prove that the four points P, Q, A' and Ha are concyclic.
References
- D. Grinberg, From Baltic Way to Feuerbach - a geometrical excursion, Mathematical Reflections 2, 2006
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
Solution
| What if applet does not run? |
We are going to establish the required fact by comparing two angles, PA'Ha and PQHa. Sometimes,depending on the configuration, the two angles are congruent and sometimes they are supplementary. In both cases the four points P, A', Q, and Ha are concyclic, but the derivations are slightly different. Luckily, there is a way to combine the two derivation into one. The device we are going to use is working directed angles modulo 180°.
Since AP is the bisector of the angle at A, P is the midpoint of segment BR with R on AC. In ΔBCR, A'P is a midline and hence parallel to the base: A'P||AC. Depending on whether A' is to the right or left of La angles ACB and PA'B are either congruent or supplementary:
| (CA, CB) = (A'P, A'Ha). |
On the other hand, since angles AHaC and AQC are both right, both Ha and Q lie on the circle with diameter AC making the four points, A, Ha, Q, C, concyclic. It follows that
| (CA, CHa) = (QA, QHa). |
But (CA, CB) and (CA, CHa) are one and the same angle and the same holds for (QA, QHa) and (QP, QHa). Therefore,
| (A'P, A'Ha) = (QP, QHa). |
And the points P, Ha, Q, A' are indeed concyclic.
The configuration has other notable properties:
- A'Q||AB.
This is shown exactly as A'P||AC.
- A'P = A'Q.
Indeed, A'P||AC making (PA', PQ) = (AC, AQ). Similarly, from A'Q||AB,
(QA', Q A) = (AB, AQ). But APQ is the bisector of angle at A so that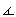 BAQ =
BAQ = 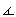 CAQ.
CAQ.A'P = A'Q. - ΔQPHa is inversely similar to ΔABC.
Indeed,
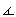 PQHa =
PQHa = 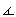 AQHa =
AQHa = 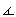 ACHa =
ACHa = 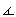 ACB. Similarly,
ACB. Similarly, 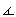 QPHa =
QPHa = 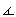 ABC.
ABC.
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73583810
