Y Can't End in a Draw

The game of Y has been invented by Craige Schensted and Charles Titus after studying Hex in 1953. Like Hex, Y is played on a board tiled with hexagonal cells. In Y, the board is triangular and the sides are not distinguished from each other in any way. Like, in Hex, two players take turns putting chips into the cells, one chip per a cell. One player plays with, say, red, the other with blue chips. Each player attempts to created a connected set of chips of his or her color that reaches to all three sides of the board.

Notably, Hex is a particular case of Y. The former is equivalent to starting Y with two corners of the board filled up with chips of two colors as shown below.

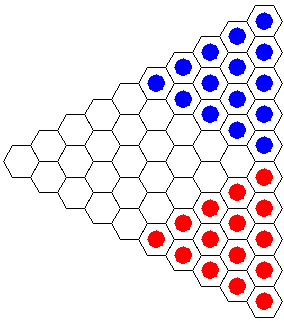
In particular, it follows that if Y can't end in a draw, a draw can't happen in Hex either.

An elegant but flawed proof of the "no-draw" property for Y has been available on the web for a long while now. The author, Jack van Rijswijck, has recently made corrections that had been included into his Ph.D. Thesis and a paper submitted for publication but had not yet reached the web. The discussion that follows is based on Jack's private communication.

The basic step in the proof is reduction by 1 of the size of the board. For a board with a single cell on a side, the assertion is obvious: the board consists of just one cell.

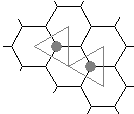
Observe that any two adjacent cells a, b have just two cells adjacent to both, call them c₁, c₂. Adjoining one of the latter to the given two forms a triangle. The two triangles abc₁ and c₂ have different orientations. In the course of the proof we are only interested in those triplets of adjacent cells whose orientation coincides with that of the board.

Let's replace each of such triplets with a single chip placed at the center of the small triangle and assign to it the color dominant in the triplet. (You'll the result of this operation if you check the "Show subgame" box in the applet below. The new chips are shown as small dots. Change the color of the chips by clicking on each of them in turn.)

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at https://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

What if applet does not run?

You can see the smaller board by pressing the "Shrink" button.

The published proof now proceeds with several claims:

A chain is a string of pieces of the same colour. Any chain in the original diagram will be preserved in the reduced diagram, because each link in the chain corresponds to a little triangle in which at least two pieces are of the same colour as the chain.
Also, if a chain touches a side in the original diagram then it will touch the same side in the reduced diagram.
Thus, winning chains will be preserved. A winning chain generates winning chains in each of the reduced diagrams, including the last one of size-1 in which a winning chain is simply the one piece on the board.
This then proves that Y cannot end in a draw. Since the piece on the size-1 board must have a colour, there must be exactly one winner in each of the previous diagrams.

You may want to ponder the weak points of the above proof before reading further.

We introduce some notations. The board of size n > 0 is denoted Y_n. B designates a 2-element set that contains one red and one blue chip. A coloring of the board assigns to every cell one of the chips from B. In other words, a coloring (of a Y_n board) is a function f: Y_n→B. So that a coloring of Y_n is an element of B^{^Y_n}. Similarly, a coloring of Y_n-1 is an element of B^{^Y_n-1}. The operation of reduction defined above is a function (n > 1)

H: B^{^Y_n} → B^{^Y_n-1}.

We shall denote the set of all colorings of Y_n in which blue is the winner by BWin_n. Similarly, we might have introduced the set RWin_n if the colorings in which red wins. The first three of the four steps in the foregoing argument show that

H: BWin_n → BWin_n-1 and
H: RWin_n → RWin_n-1,

whereas the fourth step implies that a coloring may accommodate at most one winner. What remains to be shown is that H(f) ∈ BWin_n-1 then necessarily f ∈ BWin_n, and similarly for RWin. In other words, if the operation of reduction produced a winning chain, then the original chain was bound to be winning as well.

The claim is obvious for n = 1. For a larger n, consider two adjacent cells in Y_n-1 (gray dots in the diagram below embedded in Y_n).

A straightforward enumeration of all possibilities shows that H renders the two dots the same color (blue in the diagram below) in 7 distinct configurations unique up to the symmetries of the triangular grid.

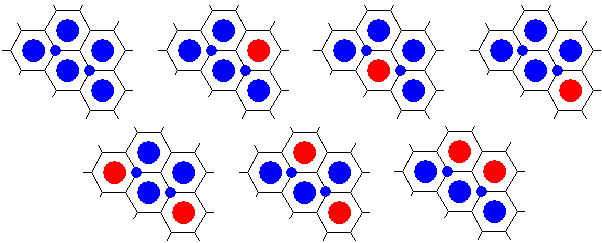
In all cases, the blue chips in Y_n form a connected set. We conclude that, for a coloring of Y_n, a connected set in H(f) might have been only produced by a connected set in f. Additionally, a boundary dot in Y_n-1 is generated by H from a triangle of chips at least two of which belong to the boundary of Y_n. At least one these is bound to have the color of the dot. It follows then, if any connected set in H(f) that reaches to the boundary of Y_n-1 owes its existence to a connected set that reaches to the related boundary of Y_n, which proves our claim: if H(f) is a blue (red) win in Y_n-1, then f is a blue (red) win in Y_n.

Remark

Steve Meyers made an observation that each n-game can be split into 3 (n-1)-games each by removing cells that form one of the three edges of the board. Further, he noticed in 2002 that the n-game is winning iff at least two of its component (n-1)-games are winning.

Remark

A more recent theory of hypergraphs also applies to the game of Y.

References

C. Browne, HEX Strategy, A K Peters, 2000
J. van Rijswijck, Theorem: Y cannot end in a draw.

The Hex and Y Games

71574329