Newton's Method

Newton might be wondering what nowadays goes under his name. Nowadays, what is known as Newton's (or Newton-Raphson) method is an iterative process set up to approximate roots of equations f(x) = 0 - a root-finding method, for short. As a matter of fact, Newton only sought to solve polynomial equations in a number of steps. (The story appears elsewhere.) But regardless, the process that now bears his name employs a great invention of his (together with Leibniz): that of the derivative of a function. For the process to be useful, one usually needs the continuity of the second derivative.

Let a be a root of the equation f(x) = 0, so that f(a) = 0. Assume f is twice continuously differentiable, Taylor's theorem gives

f(a) = f(x) + (a - x) f '(x) + (a - x)² f ''(γ)/2.

Since f(a) = 0 and assuming (a - x)² f ''(γ)/2 is small relative to the first term, we may write

0 ≈ f(x) + (a - x) f '(x)

In other words,

a ≈ x - f(x) / f '(x).

This suggests an iterative process:

(1)	xn + 1 = xn - f(xn) / f '(xn), n = 0, 1, ...

with x₀ chosen arbitrarily but hopefully in a neighborhood of the root a. The iterations have a simple geometric interpretation.

The tangent to the graph of y = f(x) at point (x_n, f(x_n)) is given by the linear equation

(2)	y = f(xn) + (x - xn) f '(xn).

The idea behind Newton's method is that the latter equation is easier to solve (even several times in a row) than the original equation f(x) = 0. Solving (2) may be expected - under certain conditions - to give a better approximation to a root a of f(x) = 0 than x_n was. So let's solve (2) for x assuming y = 0:

x = xn - f(xn) / f '(xn)

which is exactly x_{n + 1} in (1).

The applet below helps visualize the process.

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at https://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

What if applet does not run?

To start iterations click anywhere in the applet area. This defines the abcissa x₀ on the x-axis. The next click will clear the area. Once the starting point x₀ is set you can specify the number of iterations you wish to observe. The best way is to increase the number of iterations by one at a time.

Newton's iterations do not always converge. For example, they may loop up in a vicinity of a local extreme:

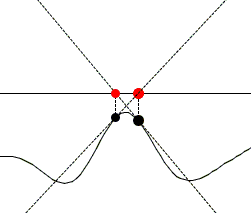
Error Analysis

Assuming f '' exists and is continuous in a vicinity of a root a of the equation f(x) = 0, Taylor's theorem gives

f(a) = f(xn) + (a - xn) f '(xn) + (a - xn)² f ''(γn)/2,

where γx_n is between a and x_n. Since f(a) = 0,

0 = f(xn) / f '(xn) + a - xn + (a - xn)² f ''(γn) / 2f '(xn).

The way Newton's iterations run, the term f(x_n) / f '(x_n) is exactly x_n - x_n+1 which gives

0 = xn - xn+1 + a - xn + (a - xn)² f ''(γn) / 2f '(xn).

Solved for a - x_n+1 the above becomes

a - xn+1 = [-f ''(γn) / 2f '(xn)] (a - xn)²

showing that the error estimate on an iteration is proportional to the square of a similar estimate on the previous iteration. Assuming that the iterates do congregate towards the root and relying on the continuity of both f ' and f '' around a, we approximate

-f ''(γn) / 2f '(xn) ≈ -f ''(a) / 2f '(a) = M

so that

a - xn+1 ≈ M (a - xn)².

This leads to

a - xn+1 ≈ [M (a - x0)]2n.

Thus, to insure convergence of the iterations, we need

|M (a - x0)| < 1

showing how close to the root the initial approximation x₀ should be chosen to insure convergence:

|a - x0| < 1 / |M|.

An Example

Let's find an approximation to √2. To this end, we may define f(x) = x² - 2, with f '(x) = 2x. In this case, the iterations (1) reduce to

xn + 1 = xn - (x²n - 2) / 2xn

or, after simplifications,

(3)	xn + 1 = ½(xn + 2 / xn).

Observe that if the iterations converge to a, i.e. if lim_n→∞x_n = a, then it follows from (3) that

a = ½(a + 2 / a)

implying a² = 2. So let's start with x₀ = 1. Then

	x1	= (1 + 2/1) / 2
		= 3/2.

Next,

	x2	= (3/2 + 2/(3/2)) / 2
		= (3/2 + 4/3) / 2
		= 17 / 12, etc

And

	x2	= (17/12 + 2/(17/12)) / 2
		= (17/12 + 24/17) / 2
		= (289 + 288) / 408
		= 577 / 408, etc.

In Java double precision the iterations appear as:

	i		xi
	0		1
	1		1.5
	2		1.4166666666666665
	3		1.4142156862745097
	4		1.4142135623746899
	5		1.414213562373095
	6		1.414213562373095

In a similar way, taking f(x) = x² - N yields

(3)	xn + 1 = ½(xn + N / xn).

as an approximation to √N. The first few iterations may well be calculated by hand.

This method for approximating square roots was known to Heron of Alexandria in the first century A.D. Already then it was possible to argue [The Princeton Companion to Mathematics, p. 110] that, since (x_n + N/x_n) / 2 is the arithmetic mean of x_n and N/x_n and since √N lies between x_n and N/x_n, x_n+1 will be close to √N if x_n is and may be closer.

References

1. K. Atkinson, Elementary Numerical Analysis, John Wiley & Sons, 1985
2. T. Gowers (ed.), The Princeton Companion to Mathematics, Princeton University Press, 2008

|Activities| |Contact| |Front page| |Contents| |Algebra|

Copyright © 1996-2018 Alexander Bogomolny