Euler's Formula and Poncelet Porism

Euler's formula that relates the circumradius, the inradius and the distance between the circumcenter and the incenter of a triangle serves the basis for the Poncelet porism for triangles.

The circumradius $R,$ the inradius $r$ and the distance between the circumcenter and the incenter $d$ of a triangle stand in an elegant relationship

$\displaystyle\frac{1}{R - d} + \frac{1}{R + d} = \frac{1}{r},$

which we shall prove in the form

$(1)\qquad 2Rr = R^{2} - d^{2}.$

Let $ABC$ be a triangle with circumcenter $O$ and incenter $I.$ Extend $AI$ to meet the circumcircle the second time at $K.$ Extend $OK$ and $OI$ to obtain two diameters $UV$ and $KK'$ of the circumcricle.

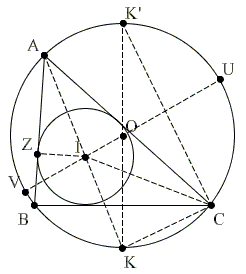
By the Intersecting Chords Theorem,

$(2)\qquad AI\cdot IK = IU\cdot IV = (R + d)(R - d) = R^{2} - d^{2}.$

Next, in $\Delta ICK,$ $\angle CIK$ is external to $\Delta ACI.$ Thus, if angles of $\Delta ABC$ are denoted $\alpha,$ $\beta,$ and $\gamma,$ we see that

$\angle CIK = (\alpha + \gamma )/2.$

On the other hand,

\( \begin{align} \angle ICK &= \angle BCI + \angle BCK \\ &= \gamma /2 + \angle BAK \\ &= \gamma /2 + \alpha /2. \\ \end{align} \)

It follows that $\angle CIK = \angle ICK$ making $\Delta ICK$ isosceles so that

$(3)\qquad IK = KC.$

Let $Z$ be the point of tangency of $AB$ and the incircle. $\Delta AIZ$ is right with angle at $A$ equal $\alpha /2.$ $\Delta CKK'$ is also right with angle at $K'$ equal $\angle CAK = \alpha /2.$ The two triangles are similar, from which we get a proportion:

$AI / IZ = KK' / KC.$

This is the same as

$(4)\qquad AI\cdot KC = IZ\cdot KK' = r\cdot 2R.$

The combination of (2), (3), and (4) yields (1). (Elsewhere there is a different proof of the formula.)

Note that a similar result holds for excircles, for example,

$(5)\qquad 2Rr_{a} = d_{a}^{2} - R^{2},$

where $r_{a}$ is the $A$-excircle and $d_{a}$ the distance between the circumcenter and the $A$-excenter.

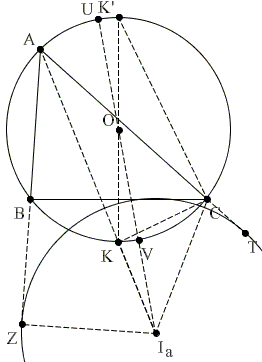
The proof must be slightly modified. For example, instead of the Intersecting Chords Theorem, we make use of the Intersecting Secants Theorem.

\( \begin{align} (d_{a} + R)(d_{a} - R) &= I_{a}U \cdot I_{a}V \\ &= I_{a}A \cdot I_{a}K \\ &= I_{a}A \cdot KC \\ &= (I_{a}Z \cdot KK'/KC) \cdot KC \\ &= r_{a} \cdot 2R. \end{align} \)

The identity can be written in an elegant way:

$(6)\qquad \displaystyle\frac{1}{d - R} - \frac{1}{d + R} = \frac{1}{r}.$

In addition,

$II_{a}^{2} = 4R(r_{a} - r),$ and
$I_{b}I_{c}^{2} = 4R(r_{b} + r_{c}).$

To see that, apply the formula for the length of a median to triangles $OII_{a}$ and $OI_{b}I_{b}:$

$OI^{2} + OI_{a}^{2} = 2 OK^{2} + II_{a}^{2}/2,$ and
$OI_{b}^{2} + OI_{c}^{2} = 2 OK'^{2} + I_{b}I_{c}^{2}/2.$

and use the just derived formulas for $OI^{2},$ $OI_{a}^{2},$ and similar.

By reversing the argument, we can establish Poncelet porism for triangles.

Poncelet Porism

If the distance $d$ between the centers of two circles $O(R)$ and $I(r)$ satisfies (1), an infinite number of triangles may be circumscribed about the circle $I(r)$ which also be inscribed in the circle $O(R).$

Indeed, from any point $A$ on $O(R)$ draw two chords $AB$ and $AC$ tangent to the circle $I(r).$ The line $AI$ bisects angle $BAC,$ and it follows from (1) that

$AI \cdot IK = 2Rr.$

From similar triangles $AIZ$ and $CKK',$

$AI \cdot CK = 2Rr,$

and therefore $IK = KC$ making $I$ the incenter of $\Delta ABC.$

Note: in a similar manner, (6) insures that a porism exists also in case where the incircle is replaced by an excircle.

References

1. N. Altshiller-Court, College Geometry, Dover, 1980, pp. 85-87
2. J. Casey, A Sequel to Euclid, Scholarly Publishing Office, University of Michigan Library (December 20, 2005), reprint of the 1888 edition, pp. 107-110
3. J. L. Coolidge, A Treatise On the Circle and the Sphere, AMS - Chelsea Publishing, 1971, p. 45
4. F. G.-M., Exercices de Géométrie, Éditions Jacques Gabay, sixiéme édition, 1991, pp. 837-839
5. R. A. Johnson, Advanced Euclidean Geometry (Modern Geometry), Dover, 1960, p. 172
6. T. Lalesco, La Géométrie du Triangle, Éditions Jacques Gabay, sixiéme édition, 1987

Resource Limit Is Reached

The website is temporarily unable to service your request as it exceeded resource limit. Please try again later.

|Contact| |Front page| |Contents| |Geometry| |Eye opener|

Copyright © 1996-2018 Alexander Bogomolny