The SSA

The acronym SSA (side-side-angle) refers to the criterion of congruence of two triangles: if two sides and an angle not include between them are respectively equal to two sides and an angle of the other then the two triangles are equal. (It is of course assumed that the equal angles at hand are adjacent to a pair of equal sides.)

Thus assume that in triangles ABC and A'B'C',

AB = A'B', AC = A'C' and ∠C = ∠C'.

Let's show that then BC = B'C'. The SSS will then imply that ΔABC = ΔA'B'C'.

Proof

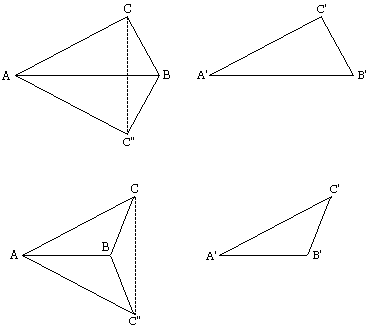
Let's place ΔA'B'C' on ΔABC so that side A'B' will coincide with AB. Let C'' will be the new position of point C'. Connect C and C''. There are two possibilities: either CC'' crosses line AB inside or outside the segment AB. In any event, Δ ACC'' is isosceles, since AC = A'C'. Consequently

∠ACC'' = ∠AC''C.

Since ∠C = ∠C'' we find, after subtracting equal angles from equal angles, that also

Whereform ΔCBC'' is isosceles. Its sides are equal: BC = BC'' and, by SSS, ΔABC = ΔABC''. It then follows that ΔABC = ΔA'B'C'.

How's that? Is everything OK? Let's discuss this.

|Contact| |Front page| |Contents| |Geometry| |Store|

Certainly there must be a mistake somewhere in the proof; for, as every one knows, the SSA is not a valid criteria for the equality of two triangles. The diagram is very much like that in Philo's proof of the SSS. And if we compare, it becomes obvious that, in our "proof" of SSA, one case is missing. Indeed, what happens if CC'' passes through B? Thinking of SSS, the effect is insignificant, but, for SSA, it makes all the difference:

Clearly, in the depicted configuration our reasoning fails.

1. A. I. Fetisov, Ya. S. Dubnov, Proof in Geometry: With "Mistakes in Geometric Proofs", Dover, (December 25) 2006

|Contact| |Front page| |Contents| |Geometry| |Store|