Pythagoras' Theorem
Elaboration on the Similarity Argument
Euclid had certainly had his reasons for supplying two proofs of the Pythagorean Theorem: I.47 and VI.31. The former, probably by the nature of it being the first and also included into the first book of the Elements, is known better by far. (E.g., the famous historian of mathematics Florian Cajori ascribes (Am Math Monthly, f 6, no 3, 1899, pp. 72-73) I.47 to Euclid himself but does not mention VI.31 at all.) Over the centuries many a proof have been invented (and re-invented) that compete in brevity or clarity with I.47. However, the less known VI.31 is second to none in its natural beauty and relevance.
The Pythagorean theorem deals with three pairs of correspondingly similar shapes. The first component in a pair is a right triangle, the second could be any shape. It's taken to be a square in I.47 and an arbitrary polygon in VI.31. The only constraint imposed on the second component is that its shape be fixed and be related in some manner to that of the first component in such a way that both change proportionally under a similarity transformation: if a generic right triangle is denoted T and S is the related shape, then, for any similarity transform,
The correspondence between the two shapes in a pair (T, S) may appear quite loose, although it is still sufficiently potent to have non-trivial implications. For example, we may claim that the ratio of areas in a pair is the same for all pairs of shapes so defined in which the first components are similar. Indeed, if T and
| (1) | Area(S) / Area(T) = Area(S') / Area(T'), |
as asserted. The claim is the result of equivalence of two view points on similarity - as scaling and as shape preservation - and has been discussed in another context. The VI.31 deals with three similar triangles, T, T' and T'' such that
whereas T' and T'' do not overlap, so that
| (2) | Area(T) = Area(T') + Area(T''). |
The Pythagorean theorem is now a consequence of the remark that, from (1),
Area(S') = m·Area(T') and
Area(S'') = m·Area(T''),
for some m > 0, such that (2) readily implies
| (3) | Area(S) = Area(S') + Area(S''), |
which is the Pythagorean Theorem if S is chosen to be the square constructed on the hypotenuse of triangle T!
Alexander Givental (Am Math Monthly, v 113, n 3, pp 261-265) offers a kindergarten version of the above argument illustrated by the applet below:
| What if applet does not run? |
Stuart Anderson has independently come up with the following argument
Start with the illustration from Proof #7. Place a point E somewhere on the figure which sits on side AB, and likewise place F and G on the figure which sit on BC and CA. Consider the following 3 figures: On side AB, the figure AEBD, i.e. the triangle ABD together with the figure lying outside the triangle on side AB. On sides BC and CA, the similar figures BFCA and CGAD. These three figures satisfy Euclid's definition of "similar and similarly described figures," and therefore we can apply the propositions from Elements Book V to them. (The figures illustrating these propositions show line segments, but Euclid clearly intended these propositions to apply to any type of magnitude at all, whether length, area, or volume.)
Therefore, by similarity
AEB : AEBD :: BFC : BFCA :: CGA : CGAD,
where the magnitudes are areas.
By Proposition V.16, and Common Notion 1,
But ABD and CAD equal BCA; therefore AEB and CGA equal BFC.
Q.E.D.
This is the "Full Euclid" way of writing the proof. The short version is that "obviously" each external figure is proportional to the internal triangle which is attached to the same side. Since the two smaller internal triangles decompose the larger, so do the two smaller external figures decompose the larger.
Alternatively, if one does not want to invoke the Book V propositions for use with areas, one can use Propositions VI.19 and VI.20 to show that the external figure and the internal triangle are each in the duplicate ratio of the side lengths, and therefore are proportional to each other. The rest of the proof is unchanged. However, I think it is cleaner to directly argue that the areas are proportional, rather than going from area ratios to length ratios and then back to area ratios, so I prefer my first version.
As a side note, both my version and the original Euclid version of Proof #7 have something in common, which dissection proofs do not share: they make it obvious why the proof requires a right angle. Of course it is because only a right triangle decomposes into 2 smaller copies which are similar to the original. The tiling proofs also show why a right angle is necessary: only right angles can fit together to form the plane tilings required for the proofs.
With dissection proofs, the reason for the right angles is sometimes obscured, and it is not clear (without some external knowledge) why the same construction could not work for some non-right triangles.
Vladmir Nikolin from Serbia seems to have found a middle ground - adding areas while applying similarity to linear dimensions:
Let D be the foot of the altitude from C of the right triangle ABC, A' be the foot of the altitude from D of the right triangle BCD and B' be the altitude from D of the right triangle ACD. If
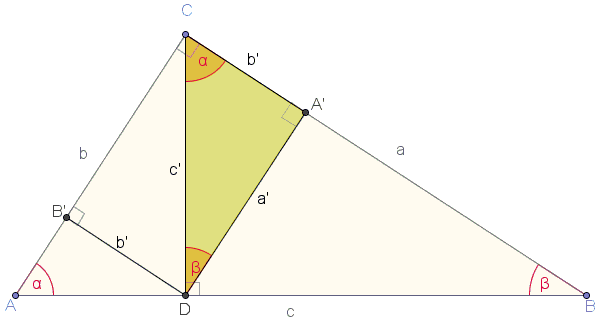
Area (ABC) = Area(ACD) + Area(BCD), so that
| c·c' / 2 | = a·a' / 2 + b·b' / 2 | |
| (4) | c·c' | = a·a' + b·b' |
It is not hard to see that triangles ABC and CDA' are similar, hence, for some
| a' | = ka | |
| b' | = kb | |
| c' | = kc |
By substitution in (4) we have:
and finally c² = a² + b².
Marc Lange, Department of Philosophy, University of North Carolina, brought to my attention the proof of the Pythagorean theorem as an application of what in the physical sciences is called dimensional reasoning. This is very close to the derivations above. I quote from [A. B. Migdal's Qualitative Methods in Quantum Theory, p. 2]
"In some case dimensional techniques actually enable one to get quantitative rather than merely qualitative results. For instance, we can prove the Pythagorean theorem purely from dimensional considerations. It follows by dimensional reasoning that the area of the triangle ABC can depend only on the square of the hypotenuse, c², multiplied by some function f(α) of the angle α. The same applies to the area of the two similar triangles ABD and BCD, but for these the hypotenuse is respectively the sides AB, BC of the large triangle. Hence
| c²f(α) = a²f(α) + b²f(α) |
which proves the theorem."
The nature of the function f(α) is inessential to the derivation as, in fact, is its dependency on the angle α. Exactly as in the opening argument, it would have sufficed to note that the area of a right triangle is proportional to the square of the hypotenuse with the coefficient of proportionality being a shape property, the shape of a right triangle being completely determined by one of the acute angles. For this reason I believe the cited treatment of the proof is somewhat confusing: it is awkward to say that a property holds for the triangle ABC and then add that "the same applies to the triangles ABD and BCD." Even introducing a function f for an expression of the area of a single triangle is rather questionable. The assertion should have been that the area of a(ny) right triangle with the hypotenuse, say, u and one of the acute angles α is obtained by dimensional reasoning to be u²f(α), which in the particular case of the triangles ABC, ABD and BCD in the diagram leads to
thus proving the theorem.
(This same proof is also included into the recent Mrs. Perkins's Electric Quilt by Paul. J. Nahin.)
At the begining of his book, Manfred Schroeder tells a fascinating story of Albert Einstein discovering this proof:
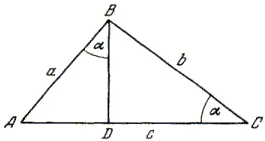
When Jacob Einstein taught (Euclidean) geometry to his 11-year-old nephew Albert, the young Einstein - even then striving for utmost parsimony - felt that some of Euclid's proofs were unnecessarily complicated. For example, in a typical proof of Pythagoras' theorem
After "a little thinking," the sharp youngster came up with a proof that required only one additional line, the altitude above the hypotenuse. This height divides the large triangle into two smaller triangles that are similar to each other and similar to the large triangle. (Triangles are similar if their angles are the same, which is easily seen to be the case.)
Now, in Euclidean geometry, the area ratio of two similar (closed) figures is equal to the square of the ratio of corresponding linear dimensions. Thus, the areas Ea, Eb, and Ec, (E as in German Ebene) of the three triangles are related to their hypotenuses a, b, and c by the following equations:
| (4) | Ea = ma² |
| (5) | Eb = mb² |
| (6) | Ec = mc² |
where m is a dimensionless nonzero multiplier that is the same in all three equations.
Now a second look at the configuration will reveal that the area of the large triangle is, of course, the sum of the areas of the two smaller triangles,
| Ea + Eb = Ec |
or, with equations (4) to (6),
| ma² + mb² = mc² |
Dividing this identity by the common measure m promptly produces Pythagoras's renowned result
| a² + b² = c² |
proved here by an 11-year old person by combining two fertile scientific principles that were going to stand the grown-up Einstein in good stead: simplicity and symmetry, of which self-similarity is a special case. Yet the true beauty of Einstein's proof is not that it is so simple, but that it exposes the true essence of Pythagoras's theorem: similarity and scaling.
The resemblance of equation (6) to Einstein's later discovery, his famous
Schroeder claims to have received "the story from Schneior Lifson of the Weizmann Institute in Tel Aviv, who has it from Einstein's assistant Ernst Strauss, to whom it was told by old Albert himself." (I'll have only one remark: the Weizmann Institute is situated in Rhovot, a city close to Tel-Aviv but not in Tel-Aviv itself.)
I can proudly add to this story one of my own. Sam Zbarsky, a 13-year relative of mine whom I mentioned in other places, was given a problem: in a right-angled triangle the altitude is drawn to the hypotenuse. The perimeter of one of the small triangle is 2, that of the given triangle 10. Find the perimeter of the second small triangle. Sam came up with the following solution.
The three triangles are similar. The areas of the triangle are in the ratio of the squares of their perimeters, say,
References
- M. Schroeder, Fractals, Chaos, Power Laws, W. H. Freeman and Co, 1991
(V.16) If four magnitudes be proportional, they will also be proportional alternately.
(In plain language: A/B = C/D implies A/C = B/D, see Nature of Pi.)
|Up| |Contact| |Front page| |Contents| |Pythagorean Theorem| |Eye opener|
Copyright © 1996-2018 Alexander Bogomolny73561269
