A Generalization of Simson Line
What Might This Be About?
Problem
Let $ABC$ be a triangle, line $\ell\,$ pass through the circumcenter $O;\,$ point $P\,$ lie on the circumcircle. Let $AP,BP,CP\,$ meet $L\,$ at $A_P, B_P, C_P,\,$ respectively. Denote $A_0,B_0,C_0\,$ the projections of $A_P, B_P, C_P\,$ onto $BC,CA,AB,\,$ respectively. Then $A_0,B_0,C_0\,$ are collinear.
Moreover, the new line passes through the midpoint of $OH,\,$ where $H\,$ the orthocenter of $\Delta ABC.\,$ If $\ell\,$ passes through $P,\,$ the line coincides with the simson.
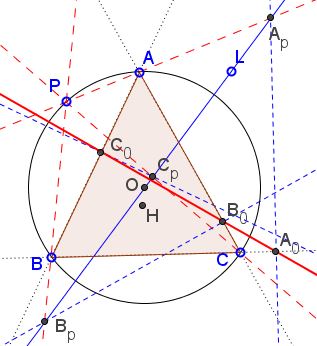
Solution 1
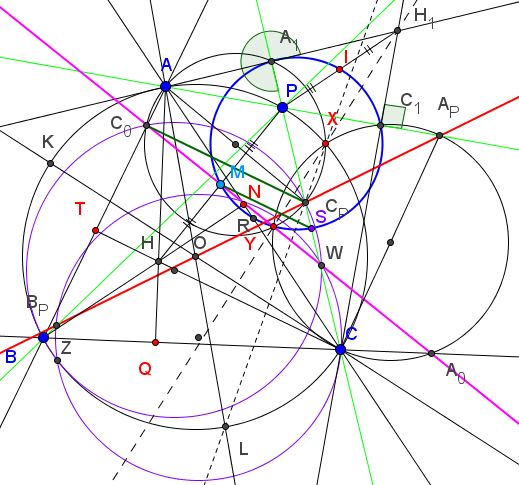
Let $X=\ell \cap AC$ and $M$ be the midpoint of $AC$. Let $Y,Z$ be the projection of $P,B$ on $AC$, respectively. Let $H_A, H_B, H_C, H_P$ be the projection of $A, B, C, P$ on $\ell$, respectively. Let $A', B', C', P'$ be the orthopole of $\ell$ with respect to $\Delta BCP, \Delta CAP, \Delta ABP, \Delta ABC$, respectively. Let $R$ be the Poncelet point of $\{ A, B, C, P \}$ (It's well-known that $R$ is the midway between $P$ and the orthocenter $H$ of $\Delta ABC).$
From a lemma at post #2 at the artofproblemsolving forum, we get $A', B', C', P'$ lie on a line $\tau$. Since $\odot (A_PA_0C )$ is the pedal circle of $A_P$ with respect to $\Delta PAC$, so from Fontene theorem we get $B' \in \odot (A_PA_0C ),$ implying $A_0, A_P, C, H_C, B'$ are concyclic.
Since $H_CA' \perp PB, H_CB' \perp PA, H_PA' \perp BC, H_PB' \perp AC$, so $\angle B'H_CA'=\angle APB=\angle ACB=\angle B'H_PA',$ from which $A', B', H_C, H_P$ are also concyclic.
From the Reim theorem and $H_PA' \parallel A_PA_0$ we get $A_0 \in A'B' \equiv \tau$ (similar discussion for $B_0, C_0).$ It's well-known that $R$ lie on the 9-point circle of $\Delta ABC$, so $P', M, Z, R$ are concyclic at the 9-point circle of $\Delta ABC$. Similarly $B', M, Y, R$ are concyclic at the 9-point circle of $\Delta ABC$. Since $B, H_B, P', X, Z$ are concyclic at the pedal circle of $X$ with respect to $\Delta ABC$, so $\angle AZP'=\angle XH_BP'=90^{\circ}-\angle (AC, \tau)$ (note that $H_BP' \perp AC).$ Similarly we can prove $\angle CYB'=90^{\circ}-\angle (AC, \tau),$ implying $ZP' \parallel YB'$, thus, from Reim theorem, we get $P', R, B'$ are collinear, i.e., $R \in \tau \equiv \overline{A_0B_0C_0}.$
Solution 2
Fix the line $\ell$ and animate $P.$ The pencils $PA,PB,PC$ are projective inducing a proyectivity on $\ell,$ i.e. the series $A_p,B_p,C_p$ are projective $\Longrightarrow$ series $A_0,B_0,C_0$ are projective.
Let $D,F$ be the antipodes of $A,C$ on the circumcircle $(O)$ and consider the case when $A_p \in BF.$ If $BC_p$ cuts $(O)$ again at $D',$ then by Pascal theorem for $APCFBD',$ it follows that $A_p,C_p,CF \cap AD'$ are collinear $\Longrightarrow$ $D \equiv D'$ $\Longrightarrow$ $\angle C_pBA=90^{\circ}$ $\Longrightarrow$ $B \equiv A_0 \equiv C_0$ $\Longrightarrow$ $A_0 \mapsto C_0$ is a perspectivity $\Longrightarrow$ $A_0C_0$ goes through a fixed point. When $P$ coincides with $\{X,Y \} \equiv \ell \cap (O),$ then $A_0C_0$ becomes Simson lines of $X,Y$ meeting at the orthopole $T$ of $\ell$ $\Longrightarrow$ $T \in A_0C_0$ and similarly $T \in B_0C_0$ $\Longrightarrow$ $A_0,B_0,C_0$ are collinear on a line $\tau$ passing through $T.$
Let $H$ be the orthocenter of $\triangle ABC$ and let $X$ be the midpoint of $HP$ lying on 9-point circle $(N).$ It's known that $T \in (N)$ when $O \in \ell.$ Now since $X \ \overline{\wedge} \ P \ \overline{\wedge} \ A_0$ with fixed points at $(N) \cap BC,$ then it follows that $X \mapsto A_0$ is a stereographic projection of $(N)$ onto $BC$ $\Longrightarrow$ $X \in TA_0 \equiv \tau.$
Solution 3
If there exists a point $W$ on the circumcircle of $\triangle{ABC}$, denote by $d_W$ the Simson line of $W$ WRT $\triangle{ABC}$ Now, let $Q$ be the reflection of $P$ WRT the line $L$ and let $M$ be the midpoint of $PH$ ($H$ is the orthocenter of $\triangle{ABC}$) We will prove that: $MA_0\parallel d_Q$.

Indeed: $T, D$ are the projections of $P, H$ on $BC$ $MP = MH \Rightarrow MD = MT$. On the other hand:
$\begin{align} (TM, TD) &= (d_P, d_S) \\ &= \frac12.\overparen{SP} \\ &= (AS, AP) \\ &= (AO, AP) \\ &= -(PO, PA) (\text{mod} \pi) \end{align}$
It follows that
(1) $\triangle{TMD} \sim \triangle{POA}.\;$
(2) $\displaystyle\frac{A_0T}{A_0D} = \frac{A_PP}{A_PA}\;$ (because $AD\parallel A_PA_0 \parallel PT)$
The two imply that $\triangle{TMA_0} \sim \triangle{POA_P},$ so that
$(MT, MA_0) = (OA_P, OP) = \frac12.\overparen{QP} = (d_P, d_Q)$ (mod $\pi$)
I.e., $\boxed{MA_0\parallel d_Q}.$
Similarly: $MB_0, MC_0 \parallel d_Q,\;$ implying $\overline{M, A_0, B_0, C_0}$ or $\overline{A_0, B_0, C_0}\;$ bisects $HP.$
Solution 4
Lemma 1 (well-known)
The two circles with diameter $AC_P , CA_P$ intersects at two points $X, Y$ , one of them (say $X$) lies on $(O)$, the second, (say $Y$ ), lies on the nine-point circle of $\triangle PAC$.}
Proof of Lemma 1
Let $CO$ cut $(O)$ again at $K$; $KA_P$ cut $(O)$ at $X$; $XC_P$ cut $(O)$ again at $L$, then by Pascal in hexagon $LAPCKX$ we get $A, O, L$ collinear. Hence $X$ lies on the circle with diameter $CA_P $ as well as the circle with diameter $AC_P $. Let the circle with diameter $AC_P$ cut $PC$ at $A_1$, the circle with diameter $CA_P$ cut $PA$ at $C_1$, then $AA_1, CC_1$ are two altitudes of $\triangle PAC$. If they intersect at $H_1$ then $H_1$ obviously lies on the radical axis of the two circles in question, thus $H_1$ lies on $XY $. Note that
$\begin{align} \angle C_1YA_1 &= \angle C_1YX + \angle XYA_1\\ &= \angle C_1CX + \angle XAH_1\\ &= 360^{\circ} - \angle AXC - \angle AH_1C\\ &= (180^{\circ}- \angle AXC) + (180^{\circ}- \angle AH_1C)\\ &= \angle APC + \angle APC\\ &=2\angle APC. \end{align}$
This means that if $I$ is the midpoint of $PH_1$ then $C_1IY A_1$ cyclic, or $Y$ lies on the nine-point circle of $\triangle PAC$.
Lemma 2
$A_0C_0$ passes through $Y$.
Proof of Lemma 2
Note that $\angle XY C_0 = \angle XAC_0 = \angle XCA_0 = \angle XYA_0$. This implies that $A_0, C_0, Y$ are collinear.
Let $AQ, CT$ the altitudes of $\triangle ABX$ with $H$ the orthocenter. Easy to get $A, H_1, C, H$ cyclic and the circle they lie on is the mirror of the circle $O$ over $AC$. If $R$ is the midpoint of $AC$ and $M$ midpoint of $PH$ then it is easy to see that R, M are the two common points of the nine-point circle of $\triangle PAC$ and the nine-point circle of $\triangle BAC$. In other words, $M$ is the midpoint of $PH$. So if $S$ is the midpoint of $PC$4 then $MS \parallel C_0C_P.$
Now we are going to show that $M $ lies on the line $Y C_0A_0$. Note that
$\begin{align} \angle{XY M} &= \angle {XY A_1} - \angle {MY A_1}\\ &= \angle XAA_1-(180 - \angle MSA_1)\\ &= \angle XAA_1-(180^{\circ} - \angle C_0C_P A_1)\\ &= \angle XAA_1 - \angle C_0AA_1\\ &= \angle XY C_0. \end{align}$
This means that $Y, M, C_0$ are collinear or $M $ lies on the line $Y C_0A_0,\;$ as desired.
Next, let the circle with diameter $CBP$ cut the circle with diameter $BC_P$ intersect at $W, Y$ . By Lemma 1, $Z$ lies on $(O)$ and $W$ lies on the nine-point circle of $PBC$. There is no problem to see that the nine-point circle of $\triangle PAC$ goes through S, M. By Lemma 2, we have $C_0, B_0, W$ collinear. Since $\angle WMS = \angle WCS = \angle WC_0C_P $ and $MS \parallel C_0C_P $, then $W, M, C_0$ are collinear. Hence all the points $A_0, C_0, M, Y, B_0, W$ lie on a line $d;\;$ this line bisects the line segment joining $P$ and the orthocenter of $\triangle BAC$ (that is $PH$). Of course then the line $l$ goes through $P$ , then $X, C_P , A_P \equiv P$ ; $P_1 \equiv Y$, $d$ is the Simson line of $\triangle ABC$.
Acknowledgment
Oai Thanh Dào posted the problem in September 2014 at the Advanced Plane Geometry group (message 1781) and subsequently at the CutTheKnotMath facebook page alnog with Telv Cohl's solution (Solution 1). Solution 2 is by Luis Gonzalez, Solution 3 by Tran Quang Huy, Solution 4 is by Tran Lam.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73566476
