Find the Center of a Given Circle

Geometric Construction with Compass Only

What Is This About?

Problem

Construct the center of a given circle.

Solution

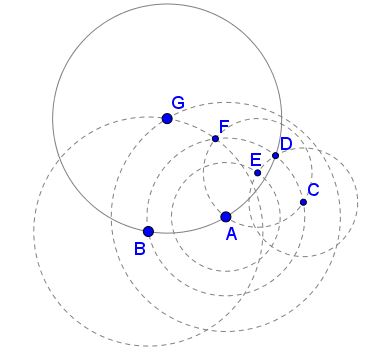
center of circle with compass only

We are given a circle. Point G will be shown to be its center. We proceed in several steps:

On the arc, choose a point A. With A as a center and an aribtrary radius, draw circle I that intersects the given arc at two points - B and D.
Use Problem #1 to construct the point C such that BC forms a diameter of the circle I.
With the radius CD draw two circles - one centered at A, another at C, and denote by E the point of their intersection.
Draw a circle of radius CD centered at E. This intersects the circle I at point F.
Now, the segment BF is the radius of the given circle whereas the two circles drawn with this radius and centers at B and A intersect at its center.

Proof

The isosceles triangles ACE and AEF are congruent, therefore ∠EAF = ∠ACE. Further, ∠BAE = ∠ACE + ∠AEC for ∠BAE is an exterior angle of the triangle ACE. Also, ∠BAE = ∠BAF + ∠EAF. Which gives ∠BAF = ∠AEC.

Thus, the isosceles triangles ABF and ACE are similar which implies BF/AB = AC/CE or BG/AB = AC/CD. It follows from the latter that the isosceles triangles ABG and ACD are also similar and, hence,

∠BAG = ∠ACD = ∠BAD/2 = ∠DAG

with the latter two equalities following from the fact that

∠BAD = ∠ADC + ∠ACD = 2∠ACD = 2∠BAG.

Since ∠BAG = ∠DAG, we conclude that the isosceles triangles ABG and ADG are congruent and, therefore, BG = AG = DG. It follows trhat the point G is the required center of the given arc.

Problems (Use a compass only)

72087599