Cantor Sets
The Cantor set C0 is a remarkable construction that is often employed to generate other useful mathematical objects. We constructed the set C0 as a limit of an iterative process. Each step of the process led to a union of closed intervals from which on the next step we removed the open middle third. The Cantor set C0 was defined as the leftover collection of points. Surprisingly uncountable, C0 has no isolated points. It's also ascribed zero length since the total length of the removed intervals is
1/3 + (2/3)(1/3) + (2/3)2(1/3) + ... = 1,
the length of the original interval [0,1]. What if we were to remove some other portion of the set, not just 1/3. What would we get when removing more than 1/3? Would we get an empty set, or a set of negative measure? The latter is absurd: since we only remove from what we have, in the "worst" case we shall remain with nothing not anything "negative".
Let's check this out. Assume we are given a number
There is a way to visualize those sets. Each is obviously self-similar consisting of two parts, the left part and the right part. Let Kk denote the set that corresponds to number k. Then
The two functions fL and fR form a 1-dimensional Iterated Function System with Kk as the fixed set. The applet below illustrates the generation of those sets. The tent function consists of two parts, the inverses of fL and fR, respectively.
The sets Kk are 1-dimensional and lie on the x-axis at the feet of black lines which are only used to make the result more salient. Due to both the limited precision of the machine arithmetic and the granularity of the display, the diagrams must be taken with a grain of salt - solely as an illustration. Also note that the functions are squashed vertically and are not drawn to scale.
To modify the value of a, drag the vertex of the tent function up and down. The allowed values of a range from a > 2 through a little beyond 4.
As of 2018, Java plugins are not supported by any browsers (find out more). This Wolfram Demonstration, Cantor Set, shows an item of the same or similar topic, but is different from the original Java applet, named 'Cantor'. The originally given instructions may no longer correspond precisely.
(image below from deprecated 'Cantor' applet)
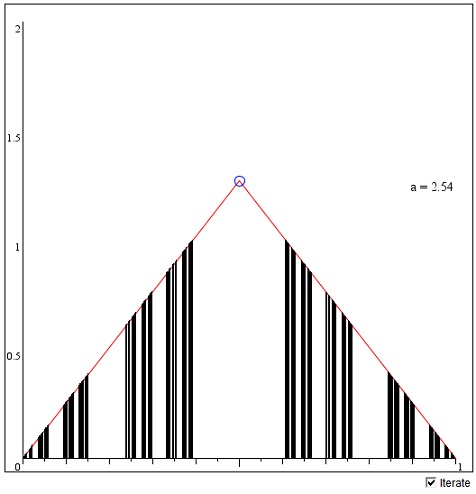
For a >2 (k < 1), the sets Kk are fractals with the similarity dimension equal to log(2)/log(a), although all have "length" 0. When a approaches 2, the dimension tends to 1, and, for
Construction of the sets Kk may be compared to the following process. Again start with the unit interval
1 - k/2 - k/4 - k/8 + ... = 1 - k > 0.
These sets are known as Cantor sets of positive measure. The Hausdorff-Besicovitch dimension of each is 1! Therefore, strictly speaking, they are not fractal. However, none of them contains an open interval however small, which is to say that the sets are nowhere dense. This follows from the fact that Cantor sets of positive measure are continuous 1-1 images of the set C0. The function that performs the job is very similar to the Cantor staircase function (although it's monotone increasing and, therefore, being continuous, is
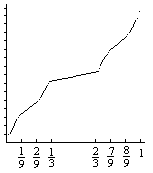
Consider C0 and a Cantor set A of positive measure. Assume on the first step we remove the interval I1 from C0 and the interval J1 from A. Map one onto the other by a linear increasing function. This is easy because the two intervals have the same center. On the second step, we remove intervals I21 and I22 from C0 and J21 and J22 from A. Map the intervals with the same indices on top of each other with linear increasing functions. Continue this process for all pairs of the removed intervals. Since, so far, the function is monotonic on the complement of C0 and C0 is nowhere dense it is possible to extend the function by continuity to the whole interval
References
- B. R. Gelbaum and J. M. H. Olmsted, Counterexamples in Analysis, Holden-Day, 1964
- B. R. Gelbaum and J. M. H. Olmsted, Theorems and Counterexamples in Mathematics, Springer-Verlag, 1990
- H.-O. Peitgen, H. Jürgens, D. Saupe, Chaos and Fractals, New Frontiers of Science, Springer, 1992
Cantor Set
- Cantor set and function
- Cantor Sets
- Difference of two Cantor sets
- Difference of two Cantor sets, II
- Sum of two Cantor sets
- Plane Filling Curves: the Lebesgue Curve
73510090 |
Copyright © 1996-2018 Alexander Bogomolny |
