C₀ + C₀ = [0, 2]

Elsewhere I suppplied 3 proofs of the fact that the differences of numbers from 2 triadic Cantor sets C₀ fills entirely the closed segment [-1, 1].

Here I'll prove the sister question, viz., that the sum of numbers from two Cantor sets fills the interval [0, 2]. There is no new mathematics involved; the idea is to reinforce the methods already used.

For two sets A and B,

A + B = {a + b : a∈A and b∈B}

I wish to prove that

C₀ + C₀ = [0, 2].

Proof #1

We'll show that every line x + y = a, where a belongs to [0, 2], intersects the product C₀×C₀. If (c, b) is the point of intersection, we automatically have b + c = a, i.e., a = b + c, where both b and c belong to the Cantor set.

The product C₀×C₀ can be constructed similarly to the Cantor set itself. Draw a 1×1 square, and divide it into 9 squares of side 1/3. Remove 5 "central" squares. Repeat the process in each of the remaining four squares. That is, divide each of them into 9 equal squares of size 1/9 and remove 5 "central" squares. And so on.

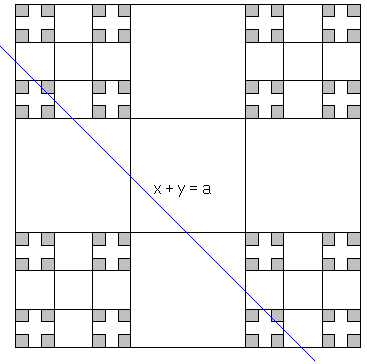
It's not hard to convince oneself that the line x + y = a intersects at least one of the 4 "corner" squares with side 1/3. Denote any of these as S₁. By the same token, any line with slope 1 that intersects the square S₁ intersects at least one of the corner squares of side length 1/9 that are contained in S₁. Denote one of them S₂. S₂⊂S₁.

In this manner we obtain a decreasing sequence {S_i} of (closed) squares. Since the sequence is decreasing, the intersection of any finite subsequence is not empty. (It's simply the smallest square in the subsequence.) This is another facet of compactness. A sequence of closed sets is said to possess a finite intersection property, if any finite subsequence has a non-empty intersection. A topological space is compact iff the intersection of every sequence of closed sets with the finite intersection property is not empty.

The original unit square being closed and bounded is compact. Therefore, the squares {S_i} have a common point. This point belongs to both C₀×C₀ and the line x + y = a.

Proof #2

Cantor set C₀ is symmetric in the midpoint of the inderval [0, 1]:

C₀ - 1/2 = 1/2 - C₀.

We thus can write,

C₀ + C₀ - 1 =
      C₀ - 1/2 + C₀ - 1/2 =
      (C₀ - 1/2) + (1/2 - C₀) =
      C₀ - C₀.

So that C₀ + C₀ = C₀ - C₀ + 1 = [-1, 1] + 1 = [0, 2].

References

1. B. R. Gelbaum and J. M. H. Olmsted, Counterexamples in Analysis, Dover, 2003
2. I. Stewart, Game, Set and Math, Penguin Books, 1989

Cantor Set

1. Cantor set and function
2. Cantor Sets
3. Difference of two Cantor sets
4. Difference of two Cantor sets, II
5. Sum of two Cantor sets
6. Plane Filling Curves: the Lebesgue Curve

|Contact| |Front page| |Contents| |Did you know?| |Geometry| |Store|