Plane Filling Curves:
All Peano Curves

The second step of Peano curve construction, when the unit square is split into 9 small squares, is the most crucial, because it defines the whole process. The pieces in two squares related to each other in the same manner regardless of the step of the construction. For example, if on the second step, a piece in square #3 is obtained from that in square #6 by means of reflection in x axis, the same will be true for pieces in squares 3 and 6 on every step of the construction.

The nine squares are ordered as shown below with the direction of traversal for each. For each of the four possible directions there are two ways to get from one corner to the opposite one in an "S" motion. The example shows the two possibilities for the traversal from the lower right corner to the upper left one.

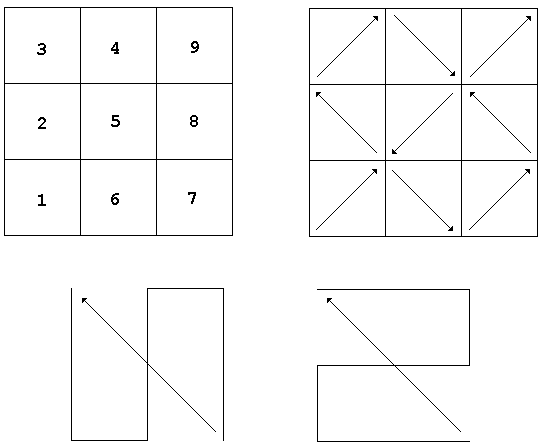
In all, there are 272 distinct curves.

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at http://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

Buy this applet
What if applet does not run?

Reference

H. Sagan, Space-Filling Curves, Springer-Verlag, 1994