Napier Bones in Various Bases

John Napier (1550-1617), a Scottish mathematician, is mostly known for his invention of logarithms - a device that revolutionized calculations by reducing difficult and tedious multiplication to addition of table entries. In 1617, three years after appearance of Mirifici logarithmorum canonis descriptio (A Description of the Wonderful Law of Logarithms), he published Rabdologiae which was recently reproduced as Rabdology by the Charles Babbage Institute in the Reprint Series for the History of Computing. The Elementary Latin Dictionary offered two entries:

1. Rab- - raving, mad, rage, be mad, ...
2. Dolo - pike, pointed stuff, sword-stick, ...

[Richard Persky from University of Texas diverges: Actually, it looks like Latinized Greek to me - rhabdos ("staff, stick") plus logos ("speech," "reason," "knowledge," "study" - it's a slippery little word with a broad range of meanings). So "Rabdologiae" would be the science of sticks, which seems a bit more reasonable than "the science of going berserk with a pointed object".]

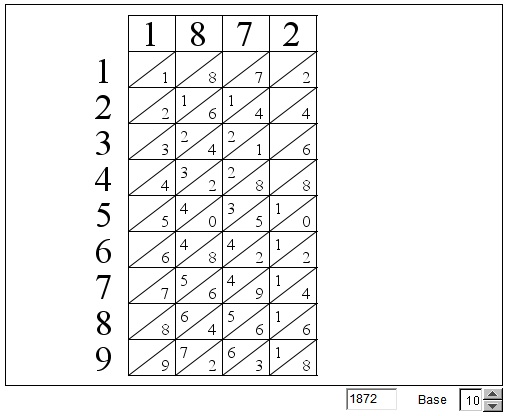
Each bone is a multiplication table for a single digit. The digit appears at the top of its bone. Below one carves consecutive products of this digit by all non-zero digits in the system (decimal in Rabdology). Each product occupies a single cell. Digits in a 2-digit number are separated, the first is written above while the second below the bottom-left top-right diagonal. To multiply 187 by 3, put three bones corresponding to digits 1,8, and 7 alongside each other. The third row looks like

The product is evaluated diagonally,

That simple. (Of course, from time to time you will have to carry 1.)

Among other wonderful things John Napier was also the discoverer of the binary system. So it's appropriate that in the applet below the base may change from 3 through 20.

References

1. H.Eves, Great Moments in Mathematics Before 1650, MAA, 1983
2. M.Gardner, Knotted Doughnuts, W.H.Freeman and Co, 1986

Copyright © 1996-2008 Alexander Bogomolny