 |
Cut The Knot!by Alex Bogomolny |
A Broken Calculator Has Its Uses
April 2000
![]()
Technological innovation has been likened to a two-faced Janus. To take an extreme example, taming of the nuclear reaction gave humanity a cheap and abundant source of energy. It also created a means of theretofore unimaginable and total destruction. A less fateful example comes from the automotive industry. A car with manual transmission can be started (if parked downhill) even with a dead battery. To start the car, shift into the second gear, keep the clutch down, release the brakes, let the car accelerate, release the clutch - and voilà! the engine starts and off you go. No need to wait for a service truck. A nice feature especially valued by forgetful people known to leave their car with lights on. On the positive side, development of the automatic transmission gave more people the freedom of movement. (At the same time, it put more bad drivers behind the steering wheel making roads more dangerous, which just serves to show how difficult it often is to unequivocally separate the benefits from the drawbacks of a new development.)
Let's turn to the controversial question of using calculators in the classroom. The question is far from being settled as becomes obvious on reading the latest issue (Volume 2, Issue 3) of the Mathematics Education Dialogues (an NCTM publication). The small volume is a collection of short articles putting forward pro and con arguments.
I'd like to make a twofold contribution to the discussion. First there is a calculator modeled after the simple calculator tool that comes standard with the Microsoft® Windows. (I expressly relieve Microsoft® from any responsibility for the performance of the model.) Later on, I shall share what I think is a very practical idea of a possible way to assess the success or failure of calculator use in the classroom.
First comes the calculator. This particular instance of the ubiquitous tool happens to malfunction. Please do not misconstrue my intention as an attempt to convey a sentiment to the effect that Good calculator is a broken calculator. Nothing would be farther from the truth. In fact, the opposite is true. Rather see in it an expression of my belief that even a broken calculator may have its uses.
In the calculator below only a few buttons are functional at any time. Obviously, the calculator cannot serve its intended general purpose. Instead, the task is to somehow compute the integers from 1 through 15 with the limited means the calculator offers. 15 numbers may be computed in any order. Those already computed will be listed in the space just above the calculator.
| What if applet does not run? |
We learn in the Dialogues that elementary mathematics curriculum may emphasize any or all of the paper-and-pencil, mental, or technology based skills. The technological wonder of the broken calculator, while helping accustom children to new technology, fosters their mental skills which I believe is the most valuable of the three.
Why so? Simply because it's the handiest of all. Once you got it it's always there, it's always available. This is utterly impractical to be dependent on a technological gadget (paper-and-pencil or a more advanced calculator) to digest all the information that one comes across in one's daily life. Naturally, some amounts of information simply exceed mental ability of an average student or a citizen. Somehow I can't worry about that. If need be, it's OK to seek a friendly advice, have a peek into an encyclopedia, or make another use of technology. But there is a minimal number of skills and basic knowledge that make a person numerate.
In his review of John Allan Paulos' Innumeracy (Vintage Books, 1990) Douglas Hofstadter wrote, "Innumeracy - the mathematical counterpart of illiteracy - is a decease that has ravaged our technological society." Please reread the previous sentence. Lamentable as the situation is, the terrible decease of innumeracy did not prevent our society from becoming and being technological. Put another way, in our society, technology and innumeracy live hand in hand.
To state the obvious, anyone who has reached the noble goal of mastering mathematics (with the use of technology or without), must have conquered along the way the common malady of innumeracy. The converse is not true. Elimination of innumeracy is therefore a more feasible goal, a necessary step on the way to achieving mathematical mastery.
My second contribution to the discussion on the use of technology in the classroom is that there should be one goal - to better teach mathematics, but two assessment practices. One is to assess mastery of the subject, the other the comfort level with the acquired mathematical tools. Let's call the latter numeracy assessment. The NCTM Standards recommend that Methods and tasks for assessing students' learning should be aligned with the curriculum. This pertains to the first kind of assessment. Numeracy assessment should be rather aligned with the age group and modest anticipation of students' knowledge. It should be carried out without any kind of technology.
For the sake of reference, here's one quote from Innumeracy (p 4):
The same people who cringe when words such as "imply" and "infer" are confused react without a trace of embarrassment to even the most egregious of numerical solecisms. I remember once listening to someone at a party drone on about the difference between "continually" and "continuously." Later that evening we were watching the news, and the TV weathercaster announced that there was a 50 percent chance of rain for Saturday and a 50 percent chance for Sunday, and concluded that there was therefore a 100 percent chance of rain that weekend. The remark went right by the self-styled grammarian, and even after I explained the mistake to him, he wasn't nearly as indignant as he would have been had the weathercaster left a dangling participle.
and another from A.K.Dewdney's 200% of Nothing (John Wiley & Sons, 1993, pp 9-10):
... a letter from a California abuse detective who finds that local, state, and other educational authorities are not above abusing percentages in the following manner: "Consider the claim: although in the seventies test scores were down nearly 60 percent, they have since rebounded by 70 percent.
Such a claim succeeds, ..., in making something out of nothing. If you listen to the numbers and don't think about them too much, it sounds like the state is doing a better job than ever. Aren't scores are 10 percent higher now than they were in the 1970s?
As a suggestion for numeracy assessment, it is reasonable to expect that 4th graders be comfortable with the addition and multiplication tables. 8th graders must be able to handle the quotes from Paulos and Dewdney with confidence. Grade 12 students should be able to detect a typo in the following passage (G. Burrill, A Revolution in My High School Classroom, Mathematics Education Dialogues, 2 (3) p13):
Calculators also make some of the things we used to do unnecessary. An example is standard deviation. Statistics texts presented the formula for standard deviation, a statistic that describes the variation of a data point from the mean, by first using the definition that highlights the difference of each data point from the mean,
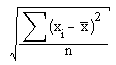
In practice, to avoid tedious computation, students were instructed to use an equivalent formula,

where the difference is not obvious. As a result, many students never really came to understand the concept.
(Numerate students should see at least 3 ways to correct the typo. This can be done by adding 1 symbol, or 2 symbols, or by lowering the center of gravity of the whole expression.)
Calculators came to the classroom in the early 1980. This is somewhat discouraging that almost 2 decades later there's still no consensus on their use. The reason I believe is in that the results of calculator usage are mixed at best. The 15 page Dialogues managed to present a spectrum of view points most of which lean on personal experience rather than a systematic study. In general, I better responded to those who tried to warn of possible pitfalls of calculator use. For what they said jibed with my personal experience. Numerate students I met and colleagues I worked with did not use calculators that much. Among students, calculator users were mostly innumerate. (Hence my suggestion to institute regular numeracy assessment tests.)
Not a single article mentioned my beloved abacus. And although I realized that it was all about calculators and not just any kind of calculating devices, I felt grouchy nonetheless. Wonderfully, one of the articles in the Dialogues (Randy Charles, p 11) supplied an explanation:
We use calculators in the elementary grades because not using them is almost certain to lead to the development of habits that are counterproductive to the development of number sense, problem solving, and positive dispositions.
That's it. For I first saw a calculator well past the graduate school.
The most congenial article Do We Need Calculators? by Kim MacKey quoted (p 3) Ralph Raimi: "Education is not imitation of life; it's an artificial process designed to put ideas into mind and not answers on paper." Hey, elementary school teachers, pay attention. The broken calculator may merit being looked into.
Related material
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny

73580872
