Infinite Border, Finite Area

Koch's snowflake is a quintessential example of a fractal curve, a curve of infinite length in a bounded region of the plane. Not every bounded piece of the plane may be associated with a numerical value called area, but the region enclosed by the Koch's curve may. Let's see why.

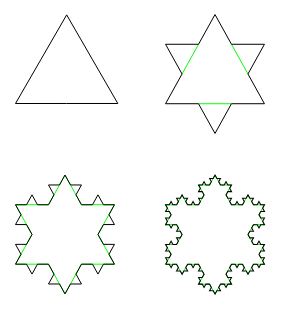
snow flake from wikipedia

We start with one triangle - a polygon or a broken line - whose boundary consists of three line segments. On each iteration, each line segment is divided into three parts and the middle part is replaced with two forming an equilateral triangle with the base removed. However, the area of these equilateral triangles is added to the area at the previous step. The areas thus accumulate and may be expected to reach a limit because the totals always remain in a bounded region.

This reasoning is sufficient for a claim of the existence of a curve of infinite length that encloses a finite area. In the particular example of Koch's curve it is not difficult to find an actual value of that area.

Recollect that the area of the equilateral triangle of side length a equals √3a²/4. Assume that the initial triangle has side length of 1 and, hence its area equals A = √3/4. The number of line segments that will undergo a transformation on the next iteration is 3, each of length 1. The first iteration adds, therefore, 3 equilateral triangles of side length 1/3 and increases the number of line segments by a factor of 4, to 12. The addon area is A × (1/3)².

The second iteration then adds 12 triangles of side length 1/3 × 1/3 = 1/3² and area A × (1/3)⁴. The number of line segments is increased to 12 × 4 = 48.

As a result of the area accumulation we obtain the following series:

S = A + A × 3 × (1/3)² + A × 3·4 × (1/3)⁴ + A × 3·4² × (1/3)⁶ + ...

Excluding the first term, we have a geometric series:

	S	= A (1 + 3/9 ∑_{n ≥ 0}(4/9)ⁿ)
		= A (1 + 1/3 × 1 / (1 - 4/9))
		= A (1 + 1/3 × 9/5)
		= A (1 + 3 /5)
		= 8A / 5.

We see that Koch's curve whose construction begins with a triangle of side 1 encloses the area of 2√3 / 5. The fact that it is finite is made starkly surprising with a thought experiment. Imagine that we have to paint the curve white in accordance with the prevailing nomenclature of Koch's snowflake. The curve being of infinite length will apparently require an infinite quantity of paint. However, only a finite quantity of paint is required to cover the finite area of the region enclosed. The paint in the region will necessarily affect the color of the boundary curve, meaning that, after all, only a finite quantity of paint is needed to paint the curve.

... to be continued ...

71867075