Maxwell's theorem links the sides and cevians in one triangle to the cevians and side lines in another:

Given two triangles ABC and MNP. Assume that the cevians in ΔABC parallel to the sides of ΔMNP are concurrent. Then the cevians in ΔMNP parallel to the sides of ΔABC are also concurrent.

Michel Cabart came up with a generalization that shows that Maxwell's theorem is of projective nature. The main tool is the projective reformulation of Ceva's theorem.

By Michel Cabart
9 May, 2008

Recollect the projective formulation of Ceva's theorem: Given an arbitrary line L, the cevians in ΔABC concur iff

where (WXYZ) denotes the cross-ratio YW/YX : ZW/ZX and the points A', B', C', A₀, B₀, C₀ are defined as in the diagram below, where L is an arbitrary straight line.

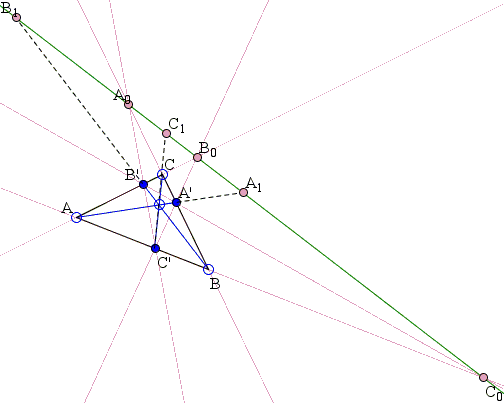
In addition, let A₁, B₁, C₁ be the intersection with L of the cevians AA', BB', and CC'.

Projection from A to the line L send the first quadruple in (1) onto B₀, C₀, A₁, A₀:

Similarly,

Thus the condition (1) can be written (cross-ratios being unchanged):

(2)	R = (A0B0C1C0)·(B0C0A1A0)·(C0A0B1B0) = -1

Proof of Maxwell's theorem

Assume there are two triangles ABC and MNP and two triples of points on L such that A₀, B₀, C₀ are intersections of L with sides of ΔABC and also with cevians of ΔMNP; A₁, B₁, C₁ are intersections of L with sides of ΔMNP and also with cevians of ΔABC.

For ΔABC, we calculate

R0 = (A0B0C1C0)·(B0C0A1A0)·(C0A0B1B0).

For ΔMNP, we calculate

R1 = (A1B1C0C1).(B1C1A0A1).(A1B1C0C1)

We have the identity R₀·R₁ = 1 (as can be seen by developing cross-ratios). Hence R₀ = -1 iff R₁ = -1, or: the cevians in ΔABC concur iff the cevians in ΔMNP concur. Choosing the infinite line as line L gives Maxwell's theorem as a particular case. The case where sides and cevians in ΔMNP are taken perpendicular (or in fact any angle) to ΔABC is straightforward via an homography (in projective terms) or a rotation (in Euclidean terms).

Note: a dynamic illustration is available on a separate page.

|Contact| |Front page| |Contents| |Store| |Geometry|

Copyright © 1996-2012 Alexander Bogomolny