The many ways to construct a triangle I

$m_{a}, m_{b}, m_{c}$

Through $A$ and $C$ draw lines parallel to $CM_{c}$ and $AM_{a},$ repsectively. Let $P$ be the point of intersection. $APCG$ is a parallelogram, so its diagonals are halved by their point of intersection. Therefore they intersect at $M_{b},$ and $CM_{b}$ is a median of $GPC.$ $PC$ is equal and parallel to $AG$ whereas $GM_{a}$ is half of $AG$ and, hence, of $PC.$ Therefore, median $GK$ of $GPC$ is parallel to $BC$ and equals $a/2.$ The third median in $GPC$ is similarly parallel to $AB$ and equals $c/2.$

Then there is the construction. Take $2/3$ of each given median. Use $SSS$ to construct the triangle $GPC.$ Find medians in this triangle. Double them. This will give the three sides of the sought triangle. Draw it again using $SSS.$
$M_{a}, M_{b}, M_{c}$

The triangle $M_{a}M_{b}M_{c}$ is similar to $\Delta ABC$ and is twice as small. Double its sides. Then use $SSS$ to construct $ABC.$
$a, b, m_{c}$

Triangle $M_{c}M_{b}C$ has the following sides: $a/2,$ $b/2,$ $m_{c}.$ It's therefore possible to construct it using $SSS.$ Now extend $CM_{b}$ to twice its length to obtain $A.$ Next, extend $AM_{c}$ to twice its length to obtain $B.$
$a, b, m_{b}$

Triangle $BM_{b}C$ is formed by the following sides: $m_{b},$ $b/2,$ $a.$ We may construct it with $SSS.$ Afterwards, extend $CM_{b}$ to twice its length to obtain $A.$
$H_{a}, H_{b}, H_{c}$

Triangle $H_{a}H_{b}H_{c}$ is known as the orthic triangle of $\Delta ABC.$ (It's the pedal triangle of the orthocenter.) Among other interesting features of the orthic triangle is the fact that the altitudes of $\Delta ABC$ are angle bisectors of $H_{a}H_{b}H_{c}.$ To prove this, note that $HH_{b}CH_{a}$ is a quadrilateral that can be inscribed into a circle with diameter $CH$ because its two angles $HH_{b}C$ and $HH_{a}C$ are both right. From here, angles $HH_{a}H_{b}$ and $ACH$ are equal. However, $ACH$ is complementary to $C$ in the triangle $ACH_{c}$ while $HH_{a}H_{b}$ is complementary to $H_{b}H_{a}C.$ Therefore, the latter is equal to $C.$ Similarly, $\angle H_{c}H_{a}B = \angle C.$ Which gives $\angle H_{c}H_{a}B = \angle H_{b}H_{a}C.$ The angles at $H_{b}$ and $H_{c}$ are handled in a similar manner.

Thus, we get the following construction. Given a triangle $H_{a}H_{b}H_{c}.$ Draw its angle bisectors. Through the vertices pass lines perpendicular to the corresponding bisectors.

(Omar X. at the old CTKExchange has noted that, if all three points are different, then the construction actually leads to four solutions. However, with right triangles in mind, the problem may have infinitely many solutions provided two of the feet coincide.)
$A, B, p$

Start with drawing a triangle $AB'C'$ with two given angles $A$ and $B.$ However you do this, the triangle you obtain will be similar to the $\Delta ABC$ we have to find. On $cc,$ starting with the point $A,$ measure the perimiter $p$ of $AB'C'$ (point $P)$ and $2p$ (point $Q).$ Connect $P$ and $C'.$ Through $Q,$ draw a line parallel to $PC'$ that intersects $bb$ at point $C.$ From $C$ draw a line parallel to $C'B'$ to obtain $B.$

A remark is in order here. Two angles completely define a triangle's shape. To determine a triangle uniquely one has to fix its size. Since in similar triangles all linear elements are in the same ratio, any linear element in a triangle uniquely determines that triangle. Therefore, the above solution will work as well in other cases. For example, when we are given $A,B,$ and, say, $l_{c}$ or $H_{a}M_{b}.$
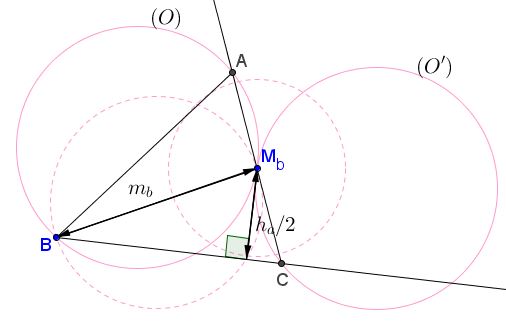
$A, m_b, h_a$

The construction is by René Sperb.

Vertex $A$ has as its locus cicle $(O)$ with chords of $BM_b$ of length $m_b$ subtending angle $A.$ Vertex $C$ is on $AM_b$ at the same distance from $M_b$ as $A,$ implying that the locus of points $C$ is circle $(O')$ symmetric to $(O)$ in $M_b.$

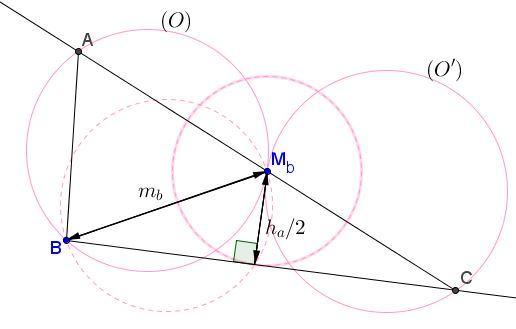
The distance from midpoint $M_b$ to side $BC$ equals $\displaystyle\frac{h_a}{2}.$ It follows that the foot of the perpendicular from $M_b$ to $BC$ lies at the intersection of circe $(BM_b)$ with diameter $BM_b$ with circle $\displaystyle C(M_b,\frac{h_a}{2}).$ The two circles always have two points of intersection. Denote one of them, say $X,$ and draw line $BX.$ That line intersects circle $(O')$ in one (when it's tangent to the circle) or two points. Either of these points may serve as vertex $C.$ Once it's selected, vertex $A$ is found as the second intersection of $CM_b$ with $(O).$ There could be $0,1,2,3,4$ solutions.

71534213