Triangle from Inradius, Circumradius, Side or Angle
Given circle $C(O,R)$ with center $O$ and radius $R,$ we'll be looking into the problem of constructing $\Delta ABC$ inscribed into $C(O,R)$ and having inradius $r.$ Assuming $R\gt 2r,$ the triangle exists and is unique, provided either one of the angles or one of the sides is given. The two problems are equivalent since equal chords in a circle subtend equal angles and vice versa. There are two constructions; one is designated as $A, R, r,$ the other $a, R, r.$
$A, R, r$
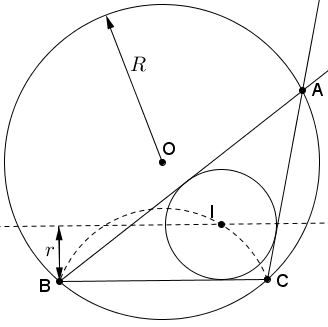
Assume the problem has been solved. Draw the inscribed and circumscribed circles. Since angle A is given, we may also assume the side BC be known. The bisectors of angles B and C intersect at the center I of the inscribed circle. $\angle B + \angle C + \angle A = 180^{\circ}.$ $\angle IBC + \angle ICB + \angle BIC = 180^{\circ}.$ Therefore, $\angle BIC = 90^{\circ} + \angle A/2.$ This means that point I belongs to a locus of points from which segment BC is seen under angle $90^{\circ} + \angle A/2.$ This is a circular arc that is easily constructed.
On the other hand, $I$ lies on the line parallel to and at the distance $r$ from $BC.$ Therefore, the point $I$ is easily determined as the intersection of a circle and a straight line.
Once $I$ has been constructed, double the angles $IBC$ and $ICB.$ Alternatively, draw the circle $C(I,r)$ with center $I$ and radius $r$, and the tangents to $C(I,r)$ from $B$ and $C.$ Point $A$ lies at the intersection of thus obtained two rays.
The construction starts with drawing the circumscribed circle and any inscribed angle equal to $A.$ This determines the segment $BC.$ Then $I$ is constructed as above and then $A.$
For a proof of correctness, just note that, by the construction, $\angle BIC=90^{\circ}+A/2,$ and drawing the tangents from $B$ and $C$ makes $BI$ and $CI$ angle bisectors in $\Delta ABC,$ implying that $\angle BAC=180^{\circ}-2(90^{\circ}-A/2)=A,$ meaning that the rays $BA$ and $CA$ meet on the circumcircle $C(O,R).$
$a, R, r$
Professor René Sperb suggested a construction that makes use of Euler's formula for the distance $d$ between the incenter and circumcenter of a triangle. The three quantities are related by $2Rr = R^{2} - d^{2}.$ It follows that $d$ could be constructed as a leg of a right triangle with the other leg $r$ and the hypotenuse $R-r.$
Note that Euler's formula explains the necessity whereas the ultimate success of the construction the sufficiency, of the condition $R\gt 2r.$
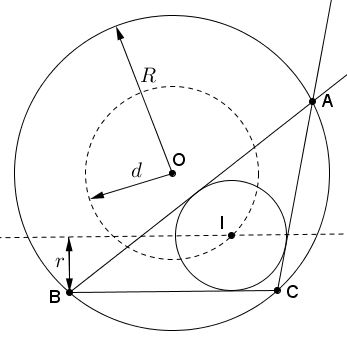
Thus we draw circles $C(O,R)$ and $C(O,d)$ of radii $R$ and $d$ around the same point $O,$ place chord $BC=a$ in the former, and path a line, say, $l\parallel BC$ at distance $r.$ The intersection of $l$ and $C(O,d)$ gives the incenter $I$ and, with it, the incircle $C(I,r).$ The tangents to the incircle from $B$ and $C$ meet at point $A$ on the circumcircle. This was obvious for the preceding construction where $\angle BIC$ was such that insured the correct value of angle at $A;$ it may be less obvious for the present one.
A proof of correctness of this construction consists in showing that the two constructions produce exactly the same circle $C(I,r).$ But this is indeed so, since, as we have seen, the first construction is correct so that, the Euler formula for the resulting $\Delta ABC$ assures that the distance $d$ for that triangle is exactly the distance used in the second construction.
We can be more explicit and derive the Euler formula along the way. First note that the arc through $B$ and $C$ used in the first construction is centered at the midpoint (I'll call it $D)$ of the arc $BC$ of circle $C(O,R).$ (This is to be expected as that arc is part of $(D)$ - a circle through the incenter.) This is indeed so because (in the diagram below) $\angle BCD = \angle CBD = A/2$ so that $\angle BDC = 180^{\circ}-A,$ making $BIC=90^{\circ}+A/2,$ for any point $I$ on the arc.
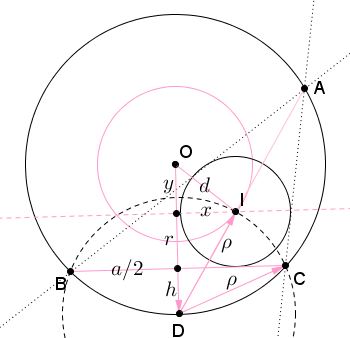
We shall now show that the distance between the $I$ found in the first construction satisfies the Euler formula, as it should. Using the notations in the diagram,
$\begin{align} y &= R - r - h,\\ x &= \sqrt{\rho^{2}-(h+r)^{2}},\\ \rho^{2} &= h^{2}+(a/2)^{2},\\ d^{2} &= x^{2}+y^{2}\\ &= \rho^{2}-(h+r)^{2}+(R-r-h)^{2}\\ &= h^{2}+(a/2)^{2}-(h+r)^{2}+(R-r-h)^{2}\\ &= (a/2)^{2}-2Rr+(R-h)^{2},\\ R^{2}&=(R-h)^{2}+(a/2)^{2} \end{align}$
Combining the last two we get $d^{2}=R^{2}-2Rr$ - the Euler formula!
|Contact| |Front page| |Contents| |Up|
Copyright © 1996-2018 Alexander Bogomolny73571791
