Property of Two Pencils of Parallel Lines

Dao Thanh Oai has posted a statement of two properties of two pencils of parallel lines at the CutTheKnotMath facebook page. One of these is a slight generalization of a previous statement; the second one is discussed below.

Let there be a of collinear points $X_0,X_1,\ldots,X_n,$ $n\ge 2.$ ($n=5$ in the diagram below.) The points also lie at the intersection of two pencils of parallel lines, say $\{l_i\}$ and $\{m_i\},$ with $i=0,1,\ldots,n$ such that $X_i=l_i\cap m_i.$ Define $Y_i=l_{i}\cap m_{i-1},$ $i=1,1,\ldots,n,$ and $C=m_0\cap l_n.$

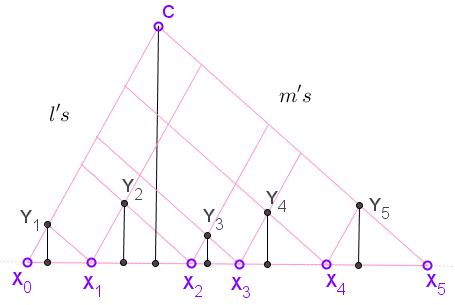
a property of two pencils of parallel lines - problem

Then the sum of distances from points $Y$ to $X_{0}X_{n}$ equals the distance from $C$ to $X_{0}X_{n}.$

If the distance from point $A$ to $X_{0}X_{n}$ is denoted $h_A$ then the statement could be expressed in the concise form:

$\displaystyle h_{C}=\sum_{i=1}^{n}h_{Y_{i}}. $

Proof 1

The proof is by induction and serves an example where a more general statement is a consequence of a more specific one.

First of all, the statement holds for $n=2.$

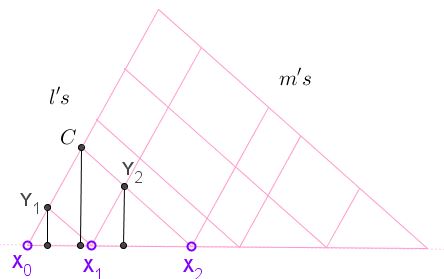
a property of two pencils of parallel lines - n=2

We have to show that $\displaystyle h_{C}=h_{Y_{1}}+h_{Y_{2}}.$ The main tool is the following property of trapezoids:

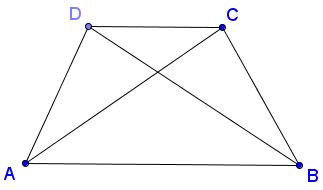
In trapezoid $ABCD,$ with $AB\parallel CD,$ $[ABD]=[ABC],$ where the brackets denote the area of the shape within.

a property of two pencils of parallel lines - n=2, solution

In particular, in trapezoid $X_{0}X_{1}Y_{2}C,$ $[X_{0}X_{1}Y_{2}]=[X_{1}Y_{2}C]$ and in trapezoid $X_{1}X_{2}CY_{1},$ $[X_{1}X_{2}Y_{1}]=[X_{1}Y_{1}C].$

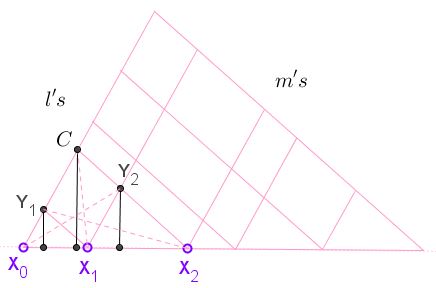
a property of two pencils of parallel lines - n=2, solution, extra

If so,

$\begin{align}\displaystyle \frac{1}{2}X_{0}X_{2}\cdot h_{C}&= [X_{0}X_{2}C]\\ &= [X_{0}X_{1}C]+[X_{1}X_{2}C]\\ &= ([X_{0}X_{1}Y_{1}]+[X_{1}Y_{1}C])+([X_{1}X_{2}Y_{2}]+[X_{1}Y_{2}C])\\ &= ([X_{0}X_{1}Y_{1}]+[X_{1}X_{2}Y_{1}])+([X_{1}X_{2}Y_{2}]+[X_{0}X_{1}Y_{2}])\\ &= [X_{0}X_{2}Y_{1}]+[X_{0}X_{2}Y_{2}]\\ &= \frac{1}{2}X_{0}X_{2}\cdot h_{Y_{1}}+\frac{1}{2}X_{0}X_{2}\cdot h_{Y_{2}}, \end{align}$

implying $\displaystyle h_{C}=h_{Y_{1}}+h_{Y_{2}}.$

Assume now that the statement holds for $n=k$ and let's prove it for $n=k+1.$ Let $C_{k}=l_{k}\cap m_{0},$ $C_{k+1}=l_{k+1}\cap m_{0},$ and $Y_{k+1}=l_{k+1}\cap m_{k}.$

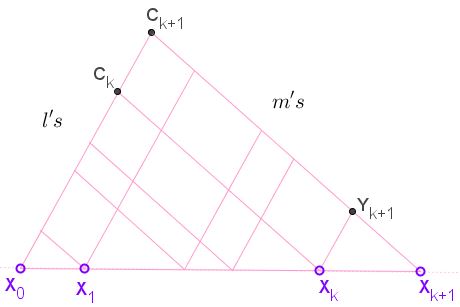
a property of two pencils of parallel lines - n=2, solution, last

This is actually a two-line configuration we have just dealt with: $h_{C_{k+1}}=h_{C_{k}}+h_{Y_{k+1}}.$ On the other hand, by the inductive assumption, $\displaystyle h_{C_{k}}=\sum_{i=1}^{k}h_{Y_{i}},$ and the conclusion follows.

Proof 2

For every $i=1,\cdot,n,$ $\Delta X_{i-1}X_{i}Y{i}$ is similar to $\Delta X_{0}X_{n}C.$ This means that certan proportions hold for all corresponding elements in the two triangles. In particular,

$\displaystyle\frac{h_{Y_{i}}}{X_{i-1}X_{i}}=\frac{h_{C}}{X_{0}X_{n}},$

in other words, $\displaystyle h_{Y_{i}}\cdot X_{0}X_{n} = h_{C}\cdot X_{i-1}X_{i}.$ Adding up gives

$\displaystyle \bigg[\sum_{i=1}^{n}h_{Y_{i}}\bigg]\cdot X_{0}X_{n} = h_{C}\cdot\bigg[\sum_{i=1}^{n} X_{i-1}X_{i}\bigg]=H_{c}\cdot X_{0}X_{n}.$

71547700