The Triangle of the Medians

The medians of a triangle form a triangle.

Proof

With a reference to the diagram below, draw $CD\parallel AM_a$ and $AD\parallel CM_c.$

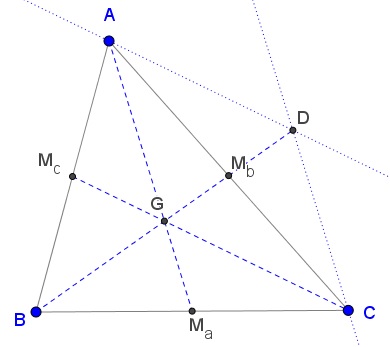
formula for the length of the median

The quadrilateral $AGCD$ is a parallelogram, so that its diagonals meet at their common midpoint, which is obviously $M_b.$ We conclude that $AD=CG=\displaystyle \frac{2}{3}m_c,$ $\displaystyle CD=AG=\frac{2}{3}m_a,$ $\displaystyle GD=2GM_b=\frac{2}{3}m_b.$ Thus the sides of $\Delta AGD$ are two thirds of the medians of $\Delta ABC.$ Dilating $\Delta AGD$ by the factors of $\displaystyle \frac{3}{2}$ we get a triangle whose sides are exactly the medians of $\Delta ABC.$

Note that the "medians'" triangle can be obtained by translating the medians, so that its angles are those originally between the medians.

Corollary

Assume in $\Delta ABC,$ $BM_b\perp CM_c.$ Then

$b^2+c^2=5a^2.$

Proof of Corollary

Since the triangle of the medians inherits the angles between them, the triangle of the medians is right, which allows us to apply the Pythagorean Theorem: $m_b^2+m_c^2=m_a^2.$ Next, we substitute into that equality the known formulas for the medians in terms of the side lengths:

$\displaystyle\begin{align} m_b^2&=\frac{1}{4}(2c^2+2a^2-b^2)\\ m_c^2&=\frac{1}{4}(2a^2+2b^2-c^2)\\ m_a^2&=\frac{1}{4}(2b^2+2c^2-a^2)\\ \end{align}$

Substituting these into the Pythagorean identity gives

$(2c^2+2a^2-b^2)+(2a^2+2b^2-c^2)=2b^2+2c^2-a^2,$

which simplifies to the required $b^2+c^2=5a^2.$

71547314