Length of a Median
Given triangle \(ABC\), with sides \(a,b,c\) opposite vertices \(A,B,C.\) The length of the median \(m_a\) from \(A\) is given by
\(\displaystyle m_{a}^{2}=\frac{b^{2}+c^{2}}{2}-\frac{a^2}{4},\) or \(\displaystyle m_{a}=\frac{1}{2}\sqrt{2(b^{2}+c^{2})-{a^2}}.\)
Here is a proof based on the Parallelogram Law:
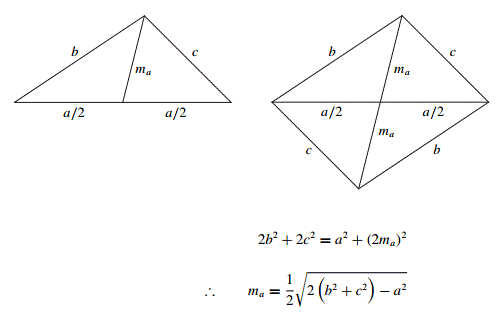
Reference
- C. P. Lawes, Proof Without Words: The Length of a Triangle Median via the Parallelogram Law, Math. Mag. 86 (2013), 146
|Contact| |Front page| |Contents| |Geometry| |Eye opener|
Copyright © 1996-2018 Alexander Bogomolny
73570678
