Triangle from Side, Inradius, and Altitude
Construct $\Delta ABC,$ given side $BC=a,$ the altitude $h_a,$ and the inradius $r.$
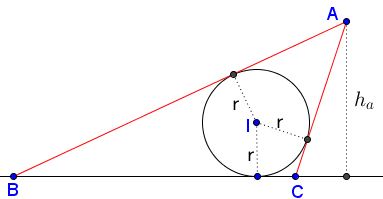
Construction
Let $s, t,u$ be the lengths of the tangents from the vertices of $\Delta ABC$ to the incircle $(I),$ as in the diagram:
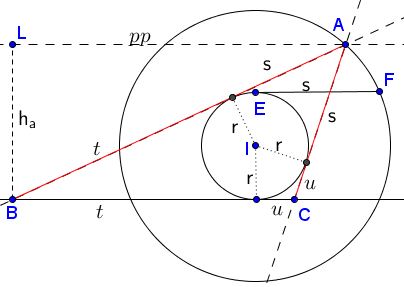
We can construct the triangle if we know the length $s.$ Indeed, drawing a tangent to $(I)$ of length $s$ ($EF$ in the diagram) we then add circle $C(I,F)$ centered at $I$ and through $F$ and find $A$ at its intersection with line $pp$ parallel to $BC$ at distance $h_a.$
To determine $s,$ we express the area $[\Delta ABC]$ of triangle $ABC$ in two ways:
$[\Delta ABC]=\frac{1}{2}a\cdot h_a$ and
$[\Delta ABC]=\frac{1}{2}[(s+t)r + (t+u)r +(u+s)r]=(s+t+u)r = (s+a)r,$
from which $s=\displaystyle\frac{a h_a}{2r}-a.$
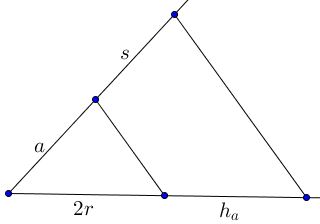
The ratio $\displaystyle\frac{a h_a}{2r}$ is easily constructed using Thales' theorem:
Acknowledgment
The construction was communicated to me by Prof. Dr. René Sperb.
|Contact| |Front page| |Contents| |Up|
Copyright © 1996-2018 Alexander Bogomolny73572058
