One Triangle from Another II
Problem
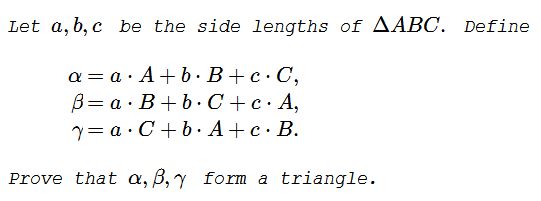
Proof 1
By the Rearrangement inequality and Euclid I.18, I.19, $\alpha\gt \beta\;$ and $\alpha\gt\gamma.\;$ Thus we only need to show that $\beta+\gamma\gt \alpha.\;$ Recollect that, since $a,b,c\;$ form a triangle, they satisfy three triangle inequalities.)
$\begin{align} \beta+\gamma &= (aB+bC+cA)+(aC+bA+cB)\\ &=(b+c)A + (c+a)B+(a+b)C\\ &\gt aA+bB+cC = \alpha, \end{align}$
as required.
Proof 2
Note that $\alpha+\beta\gt\gamma\;$ is equivalent to
$\alpha(\pi-C)+b(\pi-A)+c(\pi-B)\gt aC+bA+cB,$
or, $\alpha(\pi-2C)+b(\pi-2A)+c(\pi-2B)\gt 0.\;$ If none of the angles is obtuse, we are done. Otherwise, WLOG, assume $C\gt\displaystyle\frac{\pi}{2}.\;$ Then $A;$ and $B\;$ are acute and $c\gt a\;$ and $c\gt b.\;$ Also, $\pi-2B\gt-\pi+2C,\;$ implying $C(\pi-2B)>a(-\pi+2C),\;$ which is equivalent to
$a(\pi-2C)+b(\pi-2A)+c(\pi-2B)\gt 0.$
Similarly, we obtain the other two inequalities.
Proof 3
For a simple proof, use Ravi's substitution: $a=x+y;\;$ $b=x+z;\;$ $c=y+z\;$ which leads to
$\begin{align} \alpha+\beta-\gamma &= (x+y)(m+n-p)+(x+z)(m-n+p)+(y+z)(p+n-m)\\ &=2xm+2yn+2zp\\ &\gt 0, \end{align}$
with the other two inequalities treated similarly.
Acknowledgment
As a sequel to the previous problem, Dorin Marghidanu has kindly posted at the CutTheKnotMath facebook page another one. Leo Giugiuc's solution (Proof 2) followed almost immediately thereafter. I add another solution (Proof 1) that seem sufficiently different from Leo's.
Some time later, Dorin Marghidanu added a general statement and a proof (Proof 3) to the previous problem that also covers the present one. Marian Dinca came up with Proof 3 in a private communication.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73581298
