Segment Projections in Equilateral Triangle

Segment $PQ$ in the plane of an equilateral $\Delta ABC$ is projected on the three sides of the triangle.

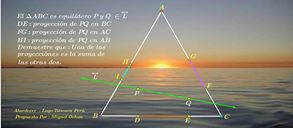
Segment Projections in Equilateral Triangle - problem

Prove that one of the projections equals the sum of the other two.

Solution

The solution is based on the observation that a projection of a segment on a given line does not change as the segment is being moved staying parallel to its initial position. Accordingly, we may choose three straight lines at $60^{\circ}$ to each other through the same point and move one of the end points of the given segment to that point.

Segment Projections in Equilateral Triangle - setup

Let $\alpha$ be the smallest angle made by the given segment and the three selected lines. Note that necessarily $0\le\alpha\le 30^{\circ}/$

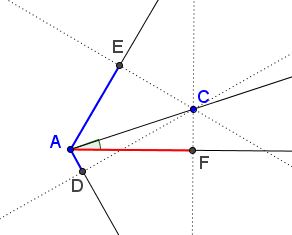
Segment Projections in Equilateral Triangle - solution

Then - assuming $AC=1$ - the three projections are given by $AE=\cos (60^{\circ}-\alpha),$ $AF=\cos \alpha,$ and $AD=\cos (60^{\circ}+\alpha),$ and the required property can b e expressed as

$\cos (60^{\circ}+\alpha)+\cos (60^{\circ}-\alpha)=\cos\alpha,$

which is an immediate application of the addition and subtraction formulas for cosine.

Acknowledgment

The problem has been posted by Miguel Ochoa Sanchez (Peru) on the CutTheKnotMath facebook page.

71921364