Third Unusual Identity in Triangle

Let $D,E,F$ denote the points of tangency of the incircle $(I)$ on the sides $BC,AC,AB$ of $\Delta ABC.$ Define $X,Y,Z$ as the points of intersection of $(I)$ with $AD,BE,CF,$ respectively.

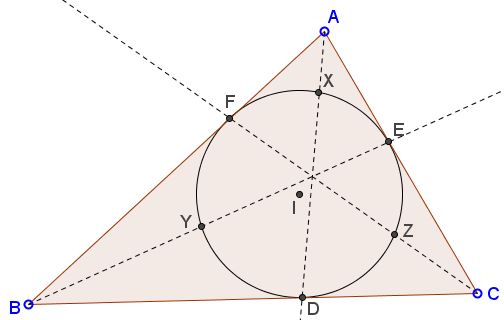
Third Unusual Identity in Triangle, problem

Prove that

$\begin{align}\displaystyle \frac{1}{\frac{AX}{XD}+\frac{1}{4}}+\frac{1}{\frac{BY}{YE}+\frac{1}{4}}+\frac{1}{\frac{CZ}{ZF}+\frac{1}{4}}=4. \end{align}$

Proof

We know that $AF = AE = p - a,$ $BD = BF = p - b,$ $CE = CD = p - c.$ Set $p - a = x,$ $p - b = y$ and $p - c = z$ such that $a = y + z,$ $b = z + x$ and $c = x + y.$

By the Power of a point theorem (applied at $A),$ $AX \cdot AD = AF^2.$ From here, $\displaystyle \frac{AX}{XD}=\frac{AD^{2}-X^{2}}{X^{2}}.$

By Stewart's theorem for the cevian $AD$ in $\Delta ABC,$

$AD^{2}(y+z)+yz(y+z)=(z+x)^{2}y+(x+y)^{2}z$

wherefrom $\displaystyle AD^{2}=x^{2}+\frac{4xyq}{y+z},$ or $\displaystyle AD^{2}-x^{2}=\frac{4xyq}{y+z}$. Combining this with the earlier identity,

$\displaystyle\frac{AX}{XD}=\frac{x^{2}}{AD^{2}-x^{2}}=\frac{x(y+z)}{4yz},$

which is equivalent to

$\displaystyle\frac{AX}{XD}+\frac{1}{4}=\frac{xy+yz+zx}{4yz}.$

In other words,

$\displaystyle\frac{1}{\frac{AX}{XD}+\frac{1}{4}}=\frac{4yz}{xy+yz+zx}.$

Similarly, $\displaystyle\frac{1}{\frac{BY}{YE}+\frac{1}{4}}=\frac{4xz}{xy+yz+zx}$ and $\displaystyle\frac{1}{\frac{CZ}{ZF}+\frac{1}{4}}=\frac{4xy}{xy+yz+zx}.$ Adding the three up gives the desired result.

Acknowledgment

The problem has been mailed to me by Leo Giugiuc along with the above proof. Leo credits the identity to Van Khea. The above joins two earlier identities by Van Khea: (1) and (2).

71939926