Seven Problems in Equilateral Triangle
Solution to Problem 2
Given an equilateral triangle $ABC$ with the base extended to twice its length: $AB'=AB.$ $B'E$ and $B'F$ are tangent to the circumcircle $(ABC).$ Let $B'I$ (with $I$ on $(ABC))$ be the second tangent from $B'$ to the incircle of $\Delta ABC,$ and $G$ the second intersection of $EF$ with the incircle.
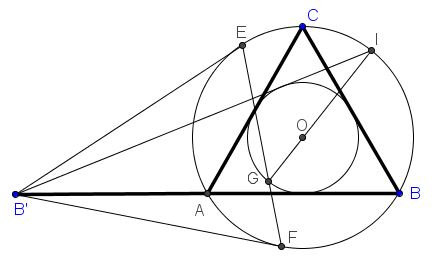
Prove that $GI$ passes through $O,$ the center of $\Delta ABC.$
Solution
$B'I$ is the reflection of $B'B$ in $BO$ and since $EF\perp B'O,$ $E$ and $F$ are the reflections of each other; in fact the segment $EF$ is its own image under the reflection. If $G$ is the image of $M$ (which, as we know, is on $EF,$ then also $MB$ is the reflection of $GI.$
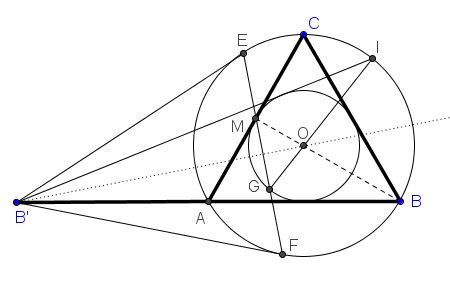
Finally, since $MB$ passes through $O,$ so does its reflection $GI.$
Acknowledgment
The proof has been suggested by Machó Bónis at the CutTheKnotMath facebook page.
|Contact| |Front page| |Contents| |Algebra| |Geometry| |Up|
Copyright © 1996-2018 Alexander Bogomolny
73579243
