A Property of Points on Excircle
Problem
$P$ is a point on the far arc of the excircle of an equilateral $\Delta ABC$ between the points of tangency. Let $[X]$ stand for the area of figure $X.$
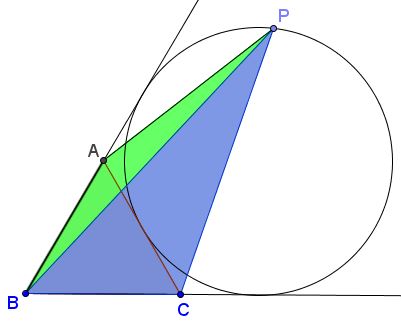
Then
$\sqrt{[ABP]} + \sqrt{[BCP]}=\sqrt{3}\sqrt{[ACP]}.$
Solution
The proof depends on two lemmas of which one has been proved elsewhere whereas the other exploits Ptolemy's theorem in the manner we learned on that page.
Lemma 1
Let $M$ be a point on a line tangent to circle $(O)$ with radius $R$ at point $N.$ $T$ a point on the circle such that $MT\perp MN.$ Denote $w=MT.$

Then $TN=\sqrt{2Rw}.$
Lemma 2
Let $D,$ $E,$ and $F$ be the points of tangency of the excircle in question with the sides of $\Delta ABC,$ as shown.
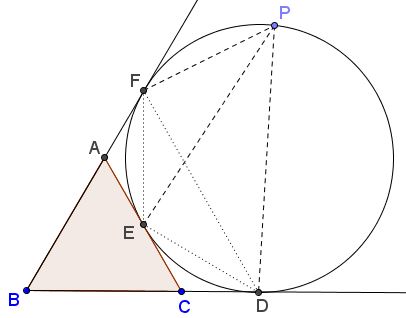
Then
$FP + DP=\sqrt{3}EP.$
This is shown by applying Ptolemy's theorem to the quadrilateral $DEFP$ and calculating explicit expressions for $DE,$ $EF,$ and $DF$ in terms of the side length of $\Delta ABC.$
Now, to solve the problem, let $x,y,z$ be the distances from $P$ to $AB,$ $BC,$ and $AC$ respectively. According to Lemma 1, $FP=\sqrt{2Rx},$ $PD=\sqrt{2Ry},$ $PE=\sqrt{2Rz},$ where $R$ is the exradius. So, for example, $\displaystyle x=\frac{1}{2R}FP^{2},$ making
$\displaystyle[ABP]=\frac{1}{2}AB\cdot x=\frac{AB}{4R}\cdot FP^{2}.$
Similarly, $\displaystyle[BCP]=\frac{BC}{4R}\cdot FD^{2}$ and $\displaystyle[ACP]=\frac{AC}{4R}\cdot FE^{2}.$ The solution follows by Lemma 2 and the fact that $AC=AB=BC.$
Acknowledgment
The problem has been posted by Miguel Ochoa Sanchez (Peru) at the CutTheKnotMath facebook page.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73565181
