Leo's Lemma, Second Application

Assume in $\Delta ABC,$ points $M$ and $N$ are on $BC$ in this order $B,M,N,C.$

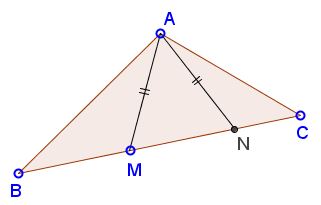
Leo's Lemma, Second Application, problem

Then $(AB-AC)(BM-CN)\ge 0.$

Proof

Assume, without loss of generality, that $AB\gt AC.$ Then $\angle ACB\gt \angle ABC.$

Since $\Delta MAN$ is isosceles, $\angle AMB=\angle ANC,$ implying that $\angle BAM\gt\angle CAN.$ Obviously, $\angle BAM +\angle CAN\lt\pi,$ implying by Leo Giugiuc's Lemma, that $\sin \angle BAM\gt\sin\angle CAN.$

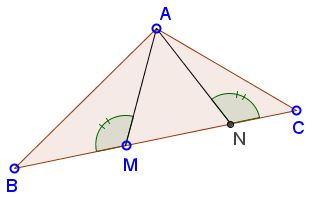
Leo's Lemma, Second Application, solution

Set $\delta =\angle AMB=\angle ANC.$ By the Law of sines, in triangles $ABM$ and $ACN,$ and due to the assumption $AB\gt AC,$

$\displaystyle\frac{BM}{\sin\angle BAM}=\frac{AB}{\sin\delta}\gt\frac{AC}{\sin\delta}=\frac{CN}{\sin\angle CAN}$

such that

$\displaystyle BM=\frac{\sin\angle BAM}{\sin\angle CAN}CN\gt CN$

because, as we've seen, $AB\gt AC$ implies $\sin\angle BAM\gt\sin\angle CAN.$

Thus, in this case, indeed, $(AB-AC)(BM-CN)\ge 0.$ The assumption $AB\lt AC$ - by symmetry - leads to the same result. The case $AB=AC$ is even more straightforward.

Acknowledgment

The statement above was posted by Leo Giugiuc at the CutTheKnotMath facebook page along with a solution of his and by Dan Sitaru - the head author - with a different solution.

They later observed that, if $M$ and $N$ are located outside the segment $BC,$ the inequality is reversed:

$(AB-AC)(BM-CN)\le 0.$

71946087