If the sum of the face angles at each vertex of a tetrahedron is 180°, prove that the tetrahedron is isosceles, i.e., the opposite edges are equal in pairs.

Solution

References

1. E. J. Barbeau, M. S. Klamkin, W. O. J. Moser, Five Hundred Mathematical Challenges, MAA, 1995, #498

|Contact| |Front page| |Contents| |Up| |Geometry| |Store|

If the sum of the face angles at each vertex of a tetrahedron is 180°, prove that the tetrahedron is isosceles, i.e., the opposite edges are equal in pairs.

Denote the vertices of the tetrahedron A, B, C, D and cut it along the edges AB, AC, AD. Unfold the tetrahedron along the remaining edges into a flat figure.

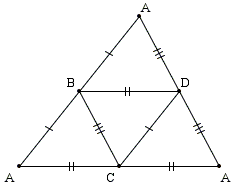
An edge along the cut will be associated with two equal segments adjacent to each other. Thus the unfolded figure ABACAD (often referred to as a map) consists of 6 pairwise equal edges. The problem tells us that the angles at each of the vertices B, C, D add up to 180°, implying that the segments in equal pairs are collinear. This means that the unfolded figure is actually a triangle ( ΔAAA) with BC, CD, DB being the midlines. Thus we immediately have, say, CD = AB and similarly BD = AC and BC = AD, as required.

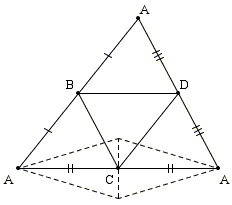
Observe that the conditions of the problem are redundant; if the face angles add up to 180° at three vertices, the fourth vertex falls in line automatically. The solution, quite naturally, made use of the condition only at the three vertices B, C, D. The diagram below shows that imposing the condition at only two vertices (B and D, in the diagram) does not suffice to insure the result.

|Contact| |Front page| |Contents| |Up| |Geometry| |Store|