Relation Engendered By Altitudes
The altitudes $AM,$ $BN,$ $CP$ divide acute $\Delta ABC$ into six smaller ones as shown:
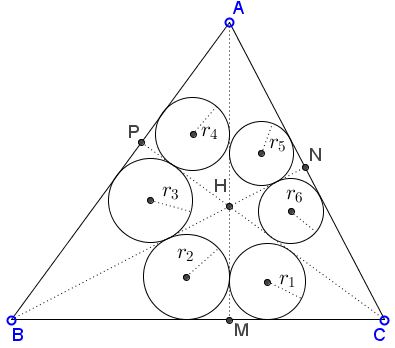
Prove that, for the inradii $r_1, \ldots, r_6$ of the small triangles, the following relation holds:
$r_1r_3r_5=r_2r_4r_6.$
Proof
First, let's recollect that, for the areas $S_1, \ldots, S_6$ of the small triangles, $S_1S_3S_5=S_2S_4S_6$ which is a direct consequence of the sine formula for the area of a triangle. We'll use this fact later. But first let's find the perimeter $p_1$ of $\Delta CHM.$
By Van Aubel's theorem, $\displaystyle\frac{AH}{HM}=\frac{AP}{PB}+\frac{AN}{NC},$ implying $\displaystyle\frac{AH}{HM}=\frac{\tan B+\tan C}{\tan A},$ i.e., $\displaystyle HM=\frac{AH\tan A}{\tan B+\tan C}.$ But $AH\tan A=a$ so that
$\displaystyle HM=\frac{a}{\tan B+\tan C}.$
On the other hand, $\displaystyle\frac{MB}{MC}=\frac{\tan C}{\tan B},$ or equivalently, $\displaystyle\frac{MC}{a}=\frac{\tan B}{\tan B+\tan C},$ implying
$\displaystyle MC=\frac{a\tan B}{\tan B+\tan C}.$
Finally, by the Pythagorean theorem in $\Delta CHM,$
$\displaystyle CH=\frac{1}{\cos B}\frac{a}{\tan B+\tan C}.$
Summing up, the perimeter of $\Delta CHM$ is given by
$\displaystyle\begin{align} p_{1}&=HM+MH+CH\\ &=\frac{a}{\cos B}\frac{1+\cos B+\sin B}{\tan B+\tan C}. \end{align}$
Thus,
$\displaystyle 2S_{1}=r_{1}\frac{a}{\cos B}\frac{1+\cos B+\sin B}{\tan B+\tan C}.$
By the same token,
$\displaystyle 2S_{3}=r_{3}\frac{c}{\cos A}\frac{1+\cos A+\sin A}{\tan A+\tan B}$
and
$\displaystyle 2S_{5}=r_{5}\frac{b}{\cos C}\frac{1+\cos C+\sin C}{\tan A+\tan C}.$
Finally,
$\displaystyle\begin{align} 2S_{1}S_{3}S_{5}&=r_{1}r_{3}r_{5}\frac{abc}{\cos A\cos B\cos C}\\ &\times\frac{(1+\cos A+\sin A)(1+\cos B+\sin B)(1+\cos C+\sin C)}{(\tan A+\tan B)(\tan B+\tan C)(\tan A+\tan C)} \end{align}$
which is symmetric in $a,b,c$ and $A,B,C,$ allowing to conclude that also
$\displaystyle\begin{align} 2S_{2}S_{4}S_{6}&=r_{2}r_{4}r_{6}\frac{abc}{\cos A\cos B\cos C}\\ &\times\frac{(1+\cos A+\sin A)(1+\cos B+\sin B)(1+\cos C+\sin C)}{(\tan A+\tan B)(\tan B+\tan C)(\tan A+\tan C)} \end{align}$
which - together with the remark made at the outset - shows that indeed $r_{1}r_{3}r_{5}=r_{2}r_{4}r_{6}.$
As a consequence, we also have $p_{1}p_{3}p_{5}=p_{2}p_{4}p_{6}$ for the perimeters of the small triangles.
Acknowledgment
The problem that is due to Gustavo Jimmy Garcia Paytan (Peru) was communicated to me along with the proof by Leo Giugiuc (Romania). The proof is by Claudia Nanuti, Diana Trailescu, Dan Sitaru and Leo Giugiuc, a Romanian crew
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73576342
