Impossiblity Condition in Concurrent Cevians
Problem

Solution 1
Let $[F]$ denote the area of shape $F.$ Introduce $x=[MBC],$ $y=[MCA]$ and $z=[MAB].$ We'll prove that if $BM\lt ME$ then $CM\gt MF.$
Indeed, by van Aubel's theorem, $\displaystyle \frac{BM}{ME}=\frac{x+z}{y},$ such that $\displaystyle \frac{x+z}{y}\gt 1$ implies $x+z\lt y$ and, from here, $y\gt x$ and $y\gt z.$
On the other hand, again by van Aubel's theorem, $\displaystyle \frac{CM}{MF}=\frac{x+y}{z}$ and, since $y\gt z,$ then of course $x+y\gt z,$ implying $CM\gt MF.$
Similarly, $CM\lt MF$ makes $BM\le ME$ impossible.
Solution 2
From Menelaus's theorem for secant $CF$ in $\Delta ABD$ and secant $BE$ in $\Delta ACF$ we have
$\displaystyle\begin{align} \frac{MD}{AM}\frac{BC}{CD}\frac{AF}{BF}&=1\\ \frac{FM}{CM}\frac{AB}{FB}\frac{CE}{AE}&=1 \end{align}$
From Ceva's theorem we have
$\displaystyle \frac{AE}{CE}\frac{CD}{BD}\frac{BF}{AF}=1$
Multiplying all above equations we obtain
$\displaystyle \frac{MD}{AM}\frac{BC}{BD}\frac{FM}{CM}\frac{AB}{FB}=1$
or
$\displaystyle \frac{BC}{BD}\frac{FM}{CM}\frac{AB}{FB}=\frac{AM}{MD}$Assuming $M$ is in the interior, $BC\gt BD$ and $AB\gt FB$, and thus if $FM\gt CM$ then $AM\gt MD$.
Solution 3
Simplest solution (without triangle). Take $A,$ $M,$ $A'$ the mirror image of $A$ in $M,$ and $D$ ordered vertically in this order from the top on ray $u$ issued from $A.$
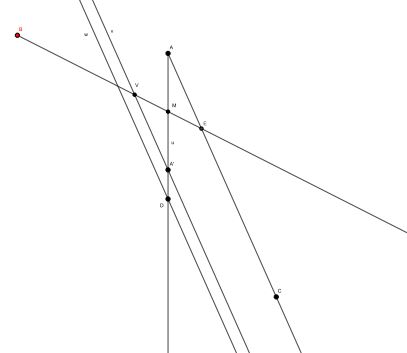
Take ray $AC$ on the right of $u,$ lines $v$ and $w$ parallel to $AC$ through $A'$ and $D,$ respectively. Take $B$ on the left of $u$ and below $w$ (this is where $B$ has to lie in the triangle!). Ray $BM$ cuts $v$ at $V$ and $AC$ at $E$ with $VM = ME:$ $BM = BV + VM$ is longer then $ME.$
Solution 4
This is a trivial corollary of what is known as Gergonne's Theorem: $\displaystyle \frac{MD}{AD}+\frac{ME}{BE}+\frac{MF}{CF}=1$ (which can be proved, for example, by areas: $\displaystyle \frac{MD}{AD} = \frac{area(BMC)}{area(ABC)},$ etc.) If any two of the inequalities in the statement were true, then the left-hand side of Gergonne's equation would be greater than $\displaystyle \frac{1}{2}+\frac{1}{2}.$
Acknowledgment
This curious observation is due to Leo Giugiuc who kindly communicated it to me, along with a proof of his. Solution 2 is by Bogdan Lataianu; Solution 3 is by Grégoire Nicollier; Solution 4 is by Vladimir Dubrovsky.
|Contact| |Up| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73578710
