Gergonne and Van Obel theorems
Ceva's theorem is a fundamental result in Triangle Geometry that relates ratios of segments cut by the concurrent cevians on the sides of a triangle. A less known result valid in the same configuration has been proved by Van Obel and bears his name. A related theorem discovered by Gergonne is virtually unknown. The latter two have simple proofs based on three observations:
The area of a triangle with a fixed base and varying apex changes in proportion to its altitude.
As a consequence of 1, if two triangles share an altitude and the base line, then their areas are in proportion to their bases.
a/b = c/d is equivalent to a/b = (a ± c)/(b ± d), unless of course
a = c andb = d.
Based on the above, I shall prove the two theorems, Gergonne's coming first:
Theorem (Gergonne, 1818)
Let three cevians AD, BE, and CF concur at a point K inside ΔABC. Then
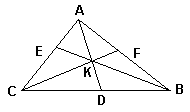
| (1) | KD/AD + KE/BE + KF/CF = 1 |
and also
| (2) | AK/AD + BK/BE + CK/CF = 2 |
Proof
Since, for example, AK/AD + KD/AD = 1, (1) and (2) are clearly equivalent. So let's prove (1).
By , Area(BKC)/Area(ABC) = KD/AD, Area(AKC)/Area(ABC) = KE/BE, Area(AKB)/Area(ABC) = KE/CE, which, when added up, yield
KD/AD + KE/BE + KF/CF = (Area(BKC) + Area(AKC) + Area(AKB))/Area(ABC) = 1.
The proof of Van Obel's theorem (often, van Aubel's theorem) takes a little longer.
Theorem (Van Obel, van Aubel)
AK/KD = AF/FB + AE/EC.
Proof
By 2, Area(AKB)/Area(BKD) = AK/KD = Area(AKC)/Area(CKD). By 3,
| (3) | AK/KD | = Area(AKB)/Area(BKD) + Area(AKC)/Area(CKD) |
| = (Area(AKB) + Area(AKC))/(Area(BKD) + Area(CKD)) | ||
| = (Area(AKB) + Area(AKC))/Area(BKC) | ||
| = Area(AKB)/Area(BKC) + Area(AKC)/Area(BKC). |
On the other hand, again by 2,
Area(ABE)/Area(BCE) = AE/EC = Area(AKE)/Area(CKE).
From here, (Area(ABE) - Area(AKE))/(Area(BCE) - Area(CKE)) = AE/EC. So that
| (4) | Area(AKB)/Area(BKC) = AE/EC. |
Similarly,
(4) and its analogues furnish an extra proof of Ceva's theorem. Indeed
| AE/EC = Area(AKB)/Area(BKC), | |
| CD/DB = Area(AKC)/Area(AKB), | |
| BF/FA = Area(BKC)/Area(AKC), |
which after multiplication give Ceva's identity.
Remark
As with barycentric coordinates, if the point K lies outside ΔABC, the areas of one or two of the triangles AKB, BKC, AKC may be regarded negative, in which case all three theorems still hold provided the segments involved are also considered signed.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73591087
