Tetrahedron with Equiareal Faces
Tetrahedron with faces of equal areas is isosceles.
One proof of this fact has been based on a simple algebraic lemma. Below is another proof kindly communicated to me by Leo Giugiuc. This proof, too, ultimately makes use of that lemma.
Let $ABCD$ be a tetrahedron. Denote with $\alpha,\beta,\gamma$ the dihedral angles between the face $ABC$ and the faces $DBC$,$DCA,$ and $DAB,$ respectively. Let $\alpha _1,\beta _1,\gamma _1$ be the dihedral angles opposites to $\alpha,\beta,\gamma,$ respectively. Denoting by $[\Delta ]$ the area of triangle $\Delta,$ we have:
$\begin{align} [ABC]&=[DBC]\cos\alpha +[DCA]\cos\beta +[DAB]\cos\gamma \\ \space[ABD]&=[CAB]\cos\gamma +[CBD]\cos\beta{_1} +[CDA]\cos\alpha{_1}\\ \space[ACD]&=[BAC]\cos\beta +[BCD]\cos\gamma{_1} +[BDA]\cos\alpha{_1} \\ \space[BCD]&=[ABC]\cos\alpha +[ACD]\cos\gamma{_1} +[ADB]\cos\beta{_1} . \end{align}$
Since the four faces are equivalent, solving the system we obtain that $\cos\alpha =\cos\alpha{_1}$, $\cos\beta =\cos\beta{_1}$ and $\cos\gamma =\cos\gamma{_1}.$ But the function $\cos:\space(0,\pi )\rightarrow\mathbb{R}$ is injective, so $\alpha =\alpha{_1},$ $\beta =\beta{_1},$ and $\gamma =\gamma{_1}.$ Obviously, the four altitudes of the tetrahedron are equal. Now let $P$ be the projection of $D$ on $ABC$ and $T$ the projection of $P$ on $BC.$
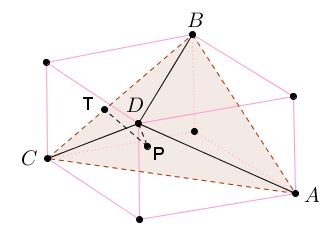
Then $DT\perp BC.$ Also consider $S$ the projection of $C$ on $ABD$ and $Q$ the projection of $S$ on $AD.$ Then $CQ\perp AD.$ We have $\Delta DPT\equiv\Delta CSQ.$ So $DT=CQ,$ and $BC=AD.$ Analogously, $AC=BD$ and $AB=CD.$
|Up| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73549356
