An Algebraic Lemma with Geometric Consequences
Lemma
Given six quantities $x,y,z,x',y',z'\,$ such that the four sums $x+y+z,\,$ $x+y'+z',\,$ $x'+y+z',\,$ and $x'+y'+z,\,$ are equal. Then $x=x',\,$ $y=y',\,$ and $z=z'.\,$
The proof is immediate. Subtract in turn from the first sum the other three to obtain three equations:
$\begin{align} (y-y')&+(z-z')=0\\ (x-x')&+(z-z')=0\\ (x-x')&+(y-y')=0. \end{align}$
Summing up gives $(x-x')+(y-y')+(z-z')=0.\;$ Subtract now from this each of the three equations: $x-x'=0,\,$ $y-y'=0,\,$ $z-z'=0,\,$ as required.
This simple lemma has several interesting applications.
Tetrahedron with isoperimetric faces
Any tetrahedron with isoperimetric faces, i.e., faces of the same perimeter, is isosceles.
For a proof, let $a,a',\,$ $b,b',\,$ $c,c'\,$ denoted the pairs of opposite edges of the tetrahedron.
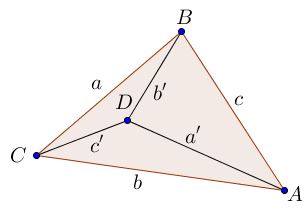
The four faces of the tetrahedron have perimeters $a+b+c,\,$ $a+b'+c',\,$ $a'+b+c',\,$ and $a'+b'+c\,$ that are equal. By direct application of the lemma, $a=a',\,$ $b=b',\,$ $c=c',\,$ as required.
Theorem of Bang
Let a sphere be inscribed in any tetrahedron. Let lines be drawn in the faces connecting the vertices with the points of tangency.
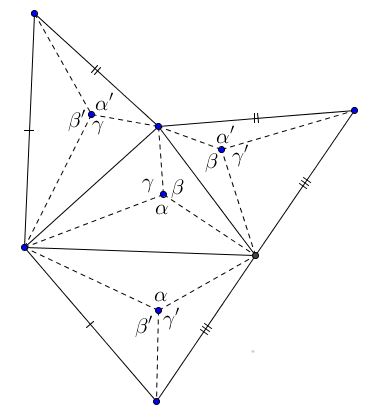
The connecting lines in a face form 3 angles which are the same in each face (Bang, 1897).
The accompanying figure shows the lines drawn in each face, the tetrahedron being opened out and developed on the plane. It is obvious that the small triangles which share a tetrahedral angle are congruent and the angles of the theorem may then be marked as in the figure. The claim is then an immediate consequence of the lemma.
Tetrahedron of equiareal faces
Theorem
If the faces of a tetrahedron have equal areas, the tetrahedron is isosceles.
Let us represent the areas of the small triangles in the figure by the letters $a, b, c; a', b', c':$
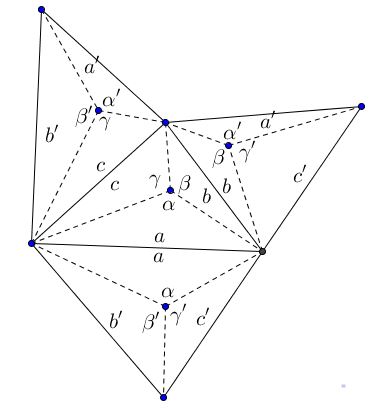
Then, by the lemma, if the faces of the tetrahedron are equiareal $a=a',\,$ $b=b',\,$ $c=c'$. Let us denote the tangential distances from the vertices to the inscribed sphere by $A, B, C, D.\,$ The equality of areas of small triangles gives three equations, a typical example of which is
$\displaystyle\frac{1}{2}A\cdot B\sin\beta =\frac{1}{2}C\cdot D\sin\beta',$
where $\beta\,$ and $\beta'\,$ are the Bang angles which were shown to be equal: $\beta =\beta'.\,$ It follows that $A\cdot B=C\cdot D.\,$ Similarly, we obtain $A\cdot C=B\cdot D\,$ and $B\cdot C=A\cdot D.$
Taking the product of the first two equations $A^{2}BC=BCD^{2}\,$ we see that $A=D.\,$ The product of the last two equations - $ABC^{2}=ABD^{2}\,$ - gives $C=D$. The product of the first and the third which is $AB^{2}C=ACD^{2}\,$ delivers $B=D\,$ such that all four quantities are equal: $A=B=C=D.$
The claim that the tetrahedron is isosceles follows readily.
Centers of the Inscribed and Circumscribed Spheres
Tetrahedron is isosceles iff the centers of its inscribed and circumscribed spheres coincide.
Isosceles tetrahedron is equifacial, thus in particular its faces are equiareal. The previous theorem implies serendipitously that incenter is equidistant from all four vertices of the tetrahedron. It follows that the incenter and circumcenter coincide.
The above argument is reversible. If the centers coincide, then the projection of the incenter on each of the faces, when joined to the vertices, splits the face into three isosceles triangles that are equal across a common edge of the tetrahedron. This causes the angles at each of the projection satisfy the lemma above, breaking the twelve small triangles into groups of equal four. From here, the tetrahedron is isosceles.
References
- B. H. Brown, Theorem of Bang. Isosceles Tetrahedra, The American Mathematical Monthly, Vol. 33, No. 4 (Apr., 1926), pp. 224-228
- Ross Honsberger, Mathematical Gems II, MAA, 1976, Chapter 9
|Up| |Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny
73579585
