Lines Crossing Circles at Vertices of Equilateral Triangle

Below we give an analytic solution to the following problem (already discussed elsewhere):

Circles $(A),$ $(B),$ $(C)$ centered at the vertices of an equilateral triangle $ABC$ with side length $4$ all have radius $\sqrt{3}.$

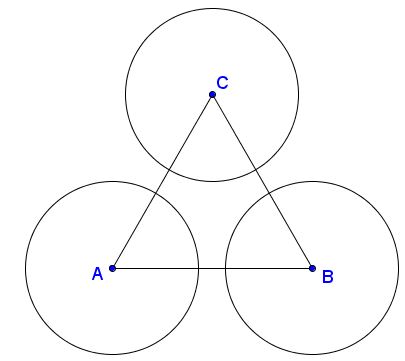
Lines through Circles at Vertices of Equilateral Triangle - problem

Describe all straight lines that have common points with all three circles.

The problem and the solution are due to Leo Giugiuc.

The solution is based on the following

Lemma

Let $d$ be a line in the plane of $\Delta ABC;$ $A',$ $B',$ $C'$ the projections of the vertices onto $d.$ Then

$[ABC]\le[A'B'C]+[AB'C']+[A'BC'],$

where $[X]$ denotes the area of figure $X.$

Either two of the projections coincide or one of the three lies between the other two. In any case, one of the segments $A'B',$ $B'C',$ $A'C'$ is the sum of the other two. Without loss of generality assume that $B'C' = A'B'+A'C'.$ More importantly, $B'C'\ge A'B'$ and $B'C'\ge A'C'.$ So, assume line $d$ has common points with all three circles. We then have:

$\begin{align}\displaystyle 2\sqrt{3} &= \frac{2[ABC]}{4}\\ &\le\frac{2([A'B'C]+[AB'C']+[A'BC'])}{4}\\ &=\frac{CC'\cdot A'B'+AA'\cdot B'C'+BB'\cdot A'C'}{4}\\ &=\frac{\sqrt{3}}{4}2B'C'\\ &\le\frac{\sqrt{3}}{4}2\sqrt{3}=2\sqrt{3}. \end{align}$

It therefore follows that for a line $d$ that meets all three circles and has $A'$ between $B'$ and $C'$, $B'C'=BC$ and $B'C'\parallel BC.$ There is just one such line. There is also one line parallel to each of the remaining two sides.

71534748