Lines through Circles at Vertices of Equilateral Triangle

Problem

Circles $(A),$ $(B),$ $(C)$ centered at the vertices of an equilateral triangle $ABC$ with side length $4$ all have radius $\sqrt{3}.$

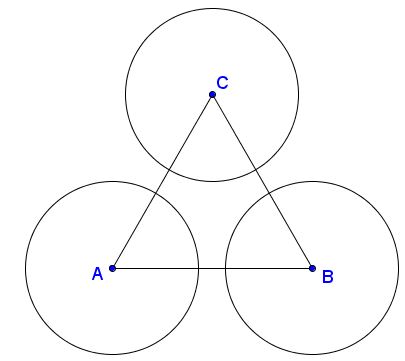
Lines through Circles at Vertices of Equilateral Triangle - problem

Describe all straight lines that have common points with all three circles.

Answer

The purpose of this writeup is to establish the following result:

Circles $(A),$ $(B),$ $(C)$ centered at the vertices of an equilateral triangle $ABC$ with side length $4,$ all have radius $\sqrt{3}.$

Lines through Circles at Vertices of Equilateral Triangle - answer

The only straight lines that have common points with all three circles are their common tangents, of which there are three.

Lemma

The midlines of $\Delta ABC$ are tangent to all three circles $(A),$ $(B),$ $(C).$

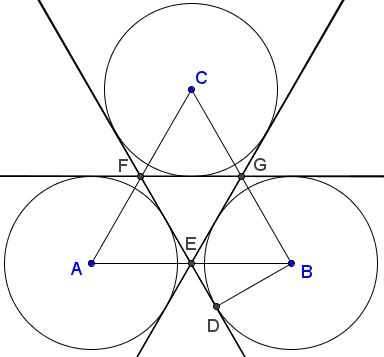
Lines through Circles at Vertices of Equilateral Triangle - lemma

For a proof, draw the common tangent of circles $(B)$ and $(C)$ on the side of $(A)$ ($EF$ in the diagram.) Let $D$ be the point of tangency on $(B)$ and $E$ the intersection of that line with $AB.$ $\Delta BDE$ is right with $\angle DBE=30^{\circ}.$ Since $BD=\sqrt{3},$ it follows that $BE=2,$ implying that $E$ is the midpoint of $AB.$

Points $F$ and $G,$ and lines $EG,$ $FG$ are constructed similarly and, by symmetry, are shown to be the common tangents to all three circles.

Solution

The proof is based on the assertion that a straight line that crosses the interior of $\Delta EG$ may at best have common points with only two of the three circles. This is because, such a line, may have common points with, say, $(A)$ only if it crosses the interior of side $EF.$ On the other hand, a straight line that pass through the interior of a triangle but not through a vertex crosses exactly two of the sides of the triangle. If a line passes through a vertex then it crosses the interior of the opposite side.

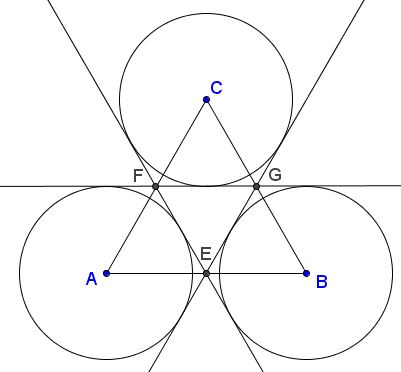
Lines through Circles at Vertices of Equilateral Triangle - solution

More transparently, a straight line that has no common points with $\Delta ABC$ may, at best, have common points with two of the circles. For example, consider a line that crosses $(A).$ If it is parallel to $EF$ it is certainly does not meet either of the remaining circles. Otherwise, it crosses line $EF$ just once outside the segment $EF$ in which case, too, it has common points with at most one of the remaining circles.

In conclusion, the only straight lines that have common points with all three circles are the midlines $EF$, $EG,$ and $FG.$

Story

The following story could be found in the book 60-odd YEARS of MOSCOW MATHEMATICAL OLYMPIADS now available online.

At the 8-th Olympiad (1945). The organizers believed that the following Problem for grade 8 was relatively easy.

Vertices $A,$ $B,$ and $C$ of triangle $ABC$ are connected with points $A',$ $B',$ and $C'$ lying on the opposite sides, but not in the vertices, as below:

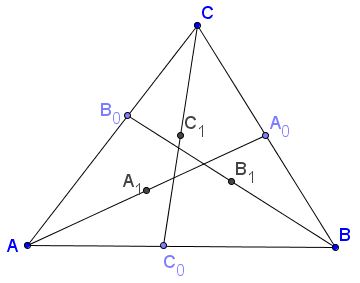
Lines through Circles at Vertices of Equilateral Triangle - story

Prove that the midpoints of segments $AA',$ $BB',$ and $CC'$ do not lie on the same straight line.

Indeed, the midpoints $A_{1},$ $B_{1},$ and $C_{1}$ in question lie sides of the medial triangle of $\Delta ABC,$ one per side. Hence, the assertion required, since no line not passing through the vertices of a triangle can cross all the sides in their inner points.

Lines through Circles at Vertices of Equilateral Triangle - story, solution

The organizers believed the statement is obvious. However, a participant, Yulik Dobrushin from the 8-th grade (now the world-famous mathematician, Roland Lvovich Dobrushin, Dr.Sc.), reached this stage in the solution and added: "For a long time I have tried to prove that a straight line cannot cross all three sides of a triangle at their inner points but failed to do so. I am horrified to realize that I do not know what a straight line is!"

Dobrushin was crowned with the first prize for this frank recognition of his failure. The members of the organizing committee might have understood the meaning of Dobrushin's phrase better than its author himself. The point is that in modern geometry the answer to the question what is a straight line is given only by listing the line's properties among which the impossibility to cross all three sides of a triangle (or an equivalent property) is usually included.

We'll look into that next.

Basics

II, 4. $A,$ $B,$ $C$ be three points that do not lie on a line and let $a$ be a line in the plane $ABC$ which does not meet any of the points $A,$ $B,$ $C.$ If the line $a$ passes through a point of the segment $AB,$ it also passes through a point of the segment $AC,$ or through a point of the segment $BC.$

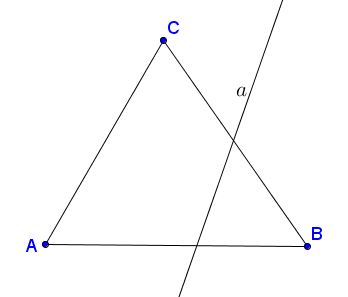
Lines through Circles at Vertices of Equilateral Triangle - basics

Expressed intuitively, if a line enters the interior of a triangle, it also leaves it. The fact that both segments $AC$ and $BC$ are not intersected by the line $a$ can be proved. (see Supplement I,1.)

From Supplement I,1.

If the line $a$ met the segments $BC,$ $CA,$ $AB$ at points $D,$ $E,$ $F$ then these points wold be distinct. By Theorem 4 one of these points would lie between the other two

If, say, $D$ lay between $E$ and $F,$ then an application of Axiom II,4 to the triangle $AEF$ and the line $BC$ would show that this line would have to pass through a point on segment $AE$ or on segment $AF.$ In both cases a contradiction of Axiom II,3 or Axiom I,2 would result.

References

D. Hilbert, Foundations of Geometry, Open Court, 1999

Acknowledgment

This problem has been posted by Leo Giugiuc (Romania) at the CutTheKnotMath facebook page.

71931817