The 80-80-20 Triangle Problem, A Variant, Solution #1
ABC is an isosceles triangle with vertex angle
Solution
Below is a solution by Mariano Perez de la Cruz.
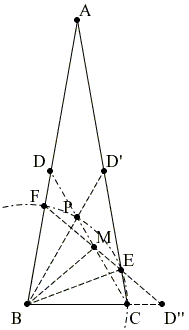
|
From point B draw a line BD', a reflection of CF the bisector of the angle at A. So BD' will form obviously 60° angle with respect to base BC like is the case for CF.
BD' intersect to CF in P; two of the angles of ΔBPC are 60°, the angle at P must be 60° too; so BPC is equilateral and all its side are equal:
BC = BP = CP. Since the arc EP of the circle is common to the angles ECP and angle EBP and since point C lies on the circle and B at its center, the central angle EBP equals twice the value of angle ECP which is 40° so the ΔBEF is equilateral too and its side EF also equals BC. So point M of intersection of EF and CD belongs to the bisector of angle CBF.
By mirroring with respect to line BM the ΔMDF we get ΔMD''C, with D'' on the extension of BC. Since angle ED''C equals 40°, angle D''EC also equals 40° which means that ΔD''CE is isosceles and side CE equals to CD'' which is the mirror image of FD. Q.E.D.

|Contact| |Front page| |Contents| |Geometry| |Up|
Copyright © 1996-2018 Alexander Bogomolny
73581860
